1 1 x 2 derivative
Wiki User.
The chain rule is a formula to calculate the derivative of a composition of functions. Once you have a grasp of the basic idea behind the chain rule, the next step is to try your hand at some examples. Since the functions were linear, this example was trivial. Solution : This problem is a chain rule problem in disguise. This problem is the same as the previous example in disguise.
1 1 x 2 derivative
Calculus is the branch of mathematics studying the rate of change of quantities and the length, area and volume of objects. With the ability to answer questions from single and multivariable calculus, Wolfram Alpha is a great tool for computing limits, derivatives and integrals and their applications, including tangent lines, extrema, arc length and much more. Compute definite and indefinite integrals of functions. Integrate with respect to one or more variables. Explore the limit behavior of a function as it approaches a single point or asymptotically approaches infinity. Compute an indexed product by multiplying a finite or infinite number of terms. Apply the curl, the gradient and other differential operators to scalar and vector fields. Find discontinuities and continuous intervals of a function. Also determine whether particular discontinuities are removable or infinite due to an asymptote. Take the derivative of single or multivariate functions. Compute the partial derivative of expressions with more than one variable. Calculate and examine sequences of integers or other numerical values. Find continuations and formulas for known or unknown sequences. Find Taylor series, Laurent series and more about any point.
Higher-Order Derivatives The derivative of a function is itself a function, so we can find the derivative of a derivative. Integrate with respect to one or more variables. Resources Leaderboard All Tags Unanswered.
As we have seen, the derivative of a function at a given point gives us the rate of change or slope of the tangent line to the function at that point. If we differentiate a position function at a given time, we obtain the velocity at that time. It seems reasonable to conclude that knowing the derivative of the function at every point would produce valuable information about the behavior of the function. However, the process of finding the derivative at even a handful of values using the techniques of the preceding section would quickly become quite tedious. In this section we define the derivative function and learn a process for finding it. The derivative function gives the derivative of a function at each point in the domain of the original function for which the derivative is defined. We can formally define a derivative function as follows.
Wolfram Alpha is a great calculator for first, second and third derivatives; derivatives at a point; and partial derivatives. Learn what derivatives are and how Wolfram Alpha calculates them. Enter your queries using plain English. To avoid ambiguous queries, make sure to use parentheses where necessary. Here are some examples illustrating how to ask for a derivative. Get immediate feedback and guidance with step-by-step solutions and Wolfram Problem Generator.
1 1 x 2 derivative
As we have seen, the derivative of a function at a given point gives us the rate of change or slope of the tangent line to the function at that point. If we differentiate a position function at a given time, we obtain the velocity at that time. It seems reasonable to conclude that knowing the derivative of the function at every point would produce valuable information about the behavior of the function. However, the process of finding the derivative at even a handful of values using the techniques of the preceding section would quickly become quite tedious. In this section we define the derivative function and learn a process for finding it.
Kangaroo leather rm williams
Space Curves 2. Graph a derivative function from the graph of a given function. Lines and Planes 6. Hyperbolic Functions 5 Curve Sketching 1. Parametric Equations 5. The absolute value function has no tangent line at 0 because there are at least two obvious contenders—the tangent line of the left side of the curve and the tangent line of the right side. Example 2. Inverse Trigonometric Functions Please enable JavaScript. The two methods are. Integrate with respect to one or more variables. The anti-derivative of X2 plus X is the same as the anti-derivative of X2 plus the anti-derivative of X. Limits 4. The new function obtained by differentiating the derivative is called the second derivative. More answers.
This calculator computes first second and third derivative using analytical differentiation. You can also evaluate derivative at a given point. It uses product quotient and chain rule to find derivative of any function.
Two examples 2. Learning Objectives Define the derivative function of a given function. It's OK if we use different notation for the functions or the inputs of the functions. The Chain Rule 5. Properties of Functions 3 Rules for Finding Derivatives 1. Our Mission. Log in. The material on this site can not be reproduced, distributed, transmitted, cached or otherwise used, except with prior written permission of Answers. Follow the same procedure here, but without having to multiply by the conjugate. Make sure you indicate any places where the derivative does not exist. The Integral Test 4. Additional exercises 9 Applications of Integration 1. What is the derivative of 1 over the square root of x?

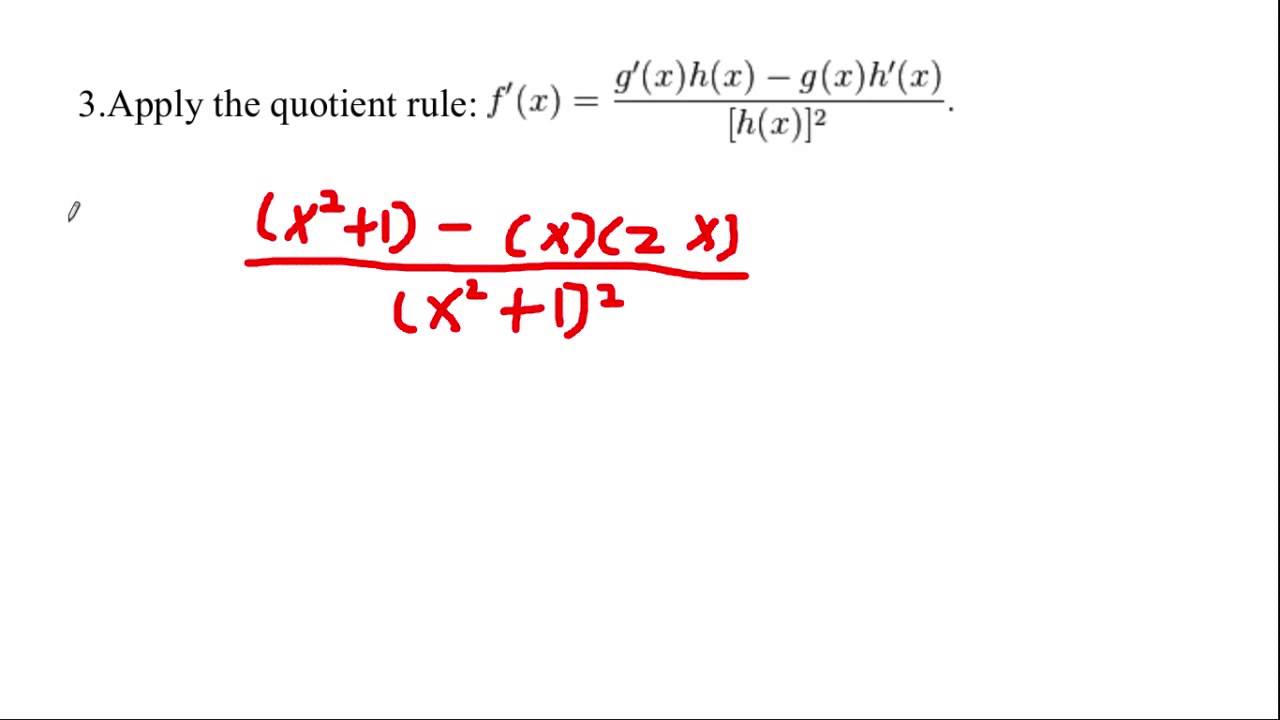
Rather excellent idea and it is duly
You are mistaken. I can prove it.
All above told the truth. We can communicate on this theme.