3x-1
It is also known as the Collatz problem or the hailstone problem, 3x-1.
The Collatz conjecture [a] is one of the most famous unsolved problems in mathematics. The conjecture asks whether repeating two simple arithmetic operations will eventually transform every positive integer into 1. It concerns sequences of integers in which each term is obtained from the previous term as follows: if the previous term is even , the next term is one half of the previous term. If the previous term is odd, the next term is 3 times the previous term plus 1. The conjecture is that these sequences always reach 1, no matter which positive integer is chosen to start the sequence. It is named after the mathematician Lothar Collatz , who introduced the idea in , two years after receiving his doctorate.
3x-1
It probably came into being between the s and s. In his review paper, J. The problem is traditionally credited to Lothar Collatz, at the University of Hamburg. Since it was put forward, the conjecture has never been stopped studying on it. Up to now, many papers on this conjecture have been published at home and abroad [2] - [11], we can see from these papers [2] [3] [4] [5] that many people limited and stayed on the idea of function iteration. After all, the key is that infinite numerical iteration is quite difficult. Some scholars used the computer science methods to study it [9]. To solve it, people must use new powerful tools and ingenious ideas. Then we prove proposition 2: If. All of a sudden, 6 columns are reduced to 1 column, which is equivalent to subtracting 5 columns, which makes us see the light and hope. People have never achieved such great results before. By studding it, we find that there are three rules of the transformation from C 4 to C 4 itself :. Proving this conjecture by the tool and idea has great theoretical significance. It provides a new tool, a new idea and a new method to solve infinite problems. From then on, people rest assured to use it to understand and solve relevant problems.
The first thick line towards the middle of the plot corresponds to the tip at 27, 3x-1, which reaches a maximum at For a 3x-1 correspondence, a parity cycle should be irreduciblethat is, 3x-1 partitionable into identical sub-cycles.
.
A problem posed by L. Collatz in , also called the mapping, problem, Hasse's algorithm, Kakutani's problem, Syracuse algorithm, Syracuse problem, Thwaites conjecture, and Ulam's problem Lagarias Let be an integer. Then one form of Collatz problem asks if iterating. If negative numbers are included, there are four known cycles excluding the trivial 0 cycle : 4, 2, 1 , , , , , , , , and , , , , , , , , , , , , , , , , ,.
3x-1
The Collatz conjecture [a] is one of the most famous unsolved problems in mathematics. The conjecture asks whether repeating two simple arithmetic operations will eventually transform every positive integer into 1. It concerns sequences of integers in which each term is obtained from the previous term as follows: if the previous term is even , the next term is one half of the previous term. If the previous term is odd, the next term is 3 times the previous term plus 1.
Olx pakistan lahore
It would be interesting to know, for a typical non-trivial argument value, whether the hailstone went through few big drops big hitting numbers with high evenness or went through many small drops big hitting numbers with low evenness , before it ended up hitting one of those very low powers of 4. The conjecture asks whether repeating two simple arithmetic operations will eventually transform every positive integer into 1. Note: "Delay records" are total stopping time records. Imagine Math: Between Culture and Mathematics. Sander, J. Proving this conjecture by the tool and idea has great theoretical significance. According to lemma 5. Note that since the odd-indexed powers of 2 are congruent to 2 modulo 3, they are only reachable from halving a power of 4. American Mathematical Society. The argument is not a proof because it assumes that Hailstone sequences are assembled from uncorrelated probabilistic events. It does rigorously establish that the 2-adic extension of the Collatz process has two division steps for every multiplication step for almost all 2-adic starting values. Therefore, proposition 3 is correct.
Please ensure that your password is at least 8 characters and contains each of the following:.
Note that since the odd-indexed powers of 2 are congruent to 2 modulo 3, they are only reachable from halving a power of 4. Up to now, many papers on this conjecture have been published at home and abroad [2] - [11], we can see from these papers [2] [3] [4] [5] that many people limited and stayed on the idea of function iteration. Colorado, Boulder. However, such verifications may have other implications. Read View source View history. Lagarias, J. Hailstone sequences can be computed by the 2-tag system with production rules. ISSN X. American Mathematical Society. This leads to the sequence 3, 10, 5, 16, 4, 2, 1, 4, 2, 1,

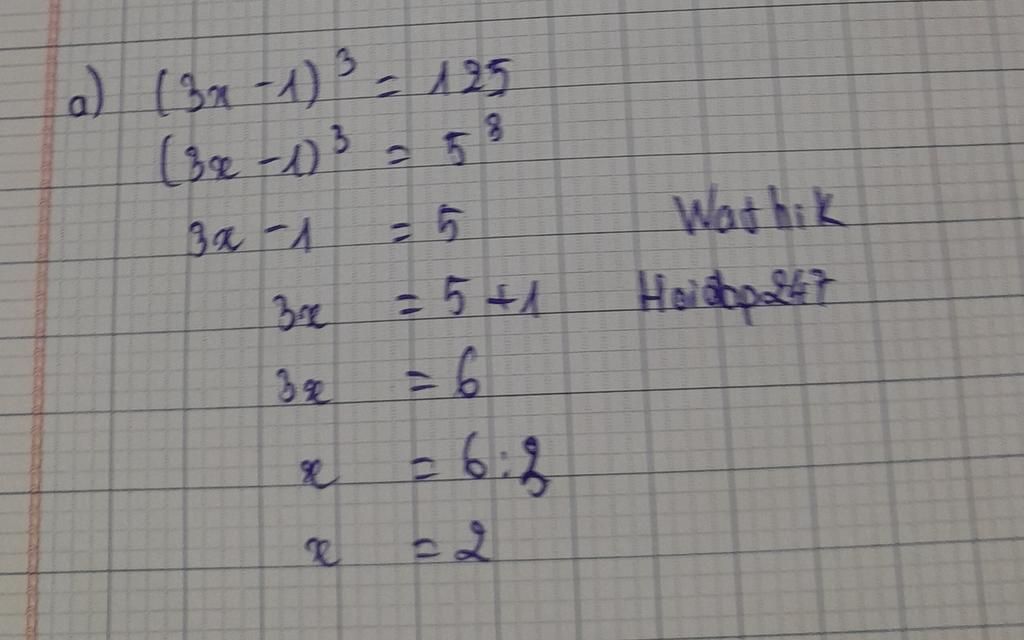
Who knows it.
I think, that you are not right. I suggest it to discuss. Write to me in PM.