Centroid of isosceles right triangle

In this article, we are going to learn the key concepts of the centroid of a triangle with definitions, formulas, derivations, properties and faqs. We have also added a few solved examples for the centroid of a triangle which candidates will find beneficial in their exam preparation, centroid of isosceles right triangle. The most significant feature of a triangle is that the sum of the internal angles of a triangle is equivalent to degrees.

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. About About this video Transcript. The centroid of a triangle is the point at which the three medians intersect. To locate the centroid, draw each of the three medians which connect the vertices of the triangle to the midpoints of the opposite sides. It is referred to as the "center of mass" or "balance point" of the triangle.

Centroid of isosceles right triangle

Every triangle has a single point somewhere near its "middle" that allows the triangle to balance perfectly, if the triangle is made from a rigid material. The centroid of a triangle is that balancing point, created by the intersection of the three medians. If the triangle were cut out of some uniformly dense material, such as sturdy cardboard, sheet metal, or plywood, the centroid would be the spot where the triangle would balance on the tip of your finger. Centroids may sound like big rocks from outer space, but they are actually important features of triangles. They also have applications to aeronautics, since they relate to the center of gravity CG of shapes. The median of a triangle is the line segment created by joining one vertex to the midpoint of the opposite side, like this:. To find the centroid of any triangle, construct line segments from the vertices of the interior angles of the triangle to the midpoints of their opposite sides. These line segments are the medians. Their intersection is the centroid. The centroid has an interesting property besides being a balancing point for the triangle. This is true for every triangle.

Important Links. The y-coordinate is going to b plus 0 plus 0. Downvote Button navigates to signup page.

In Geometry, the centroid is an important concept related to a triangle. A triangle is a three-sided bounded figure with three interior angles. Based on the sides and angles, a triangle can be classified into different types such as. The centroid is an important property of a triangle. Let us discuss the definition of centroid, formula, properties and centroid for different geometric shapes in detail. The centroid is the centre point of the object. The point in which the three medians of the triangle intersect is known as the centroid of a triangle.

Forgot password? New user? Sign up. Existing user? Log in.

Centroid of isosceles right triangle

An isosceles right triangle is a right-angled triangle whose base and height legs are equal in length. It is a type of special isosceles triangle where one interior angle is a right angle and the remaining two angles are thus congruent since the angles opposite to the equal sides are equal. It is also known by the name of right-angled isosceles triangle or a right isosceles triangle.

4325 s padre island dr corpus christi tx 78411

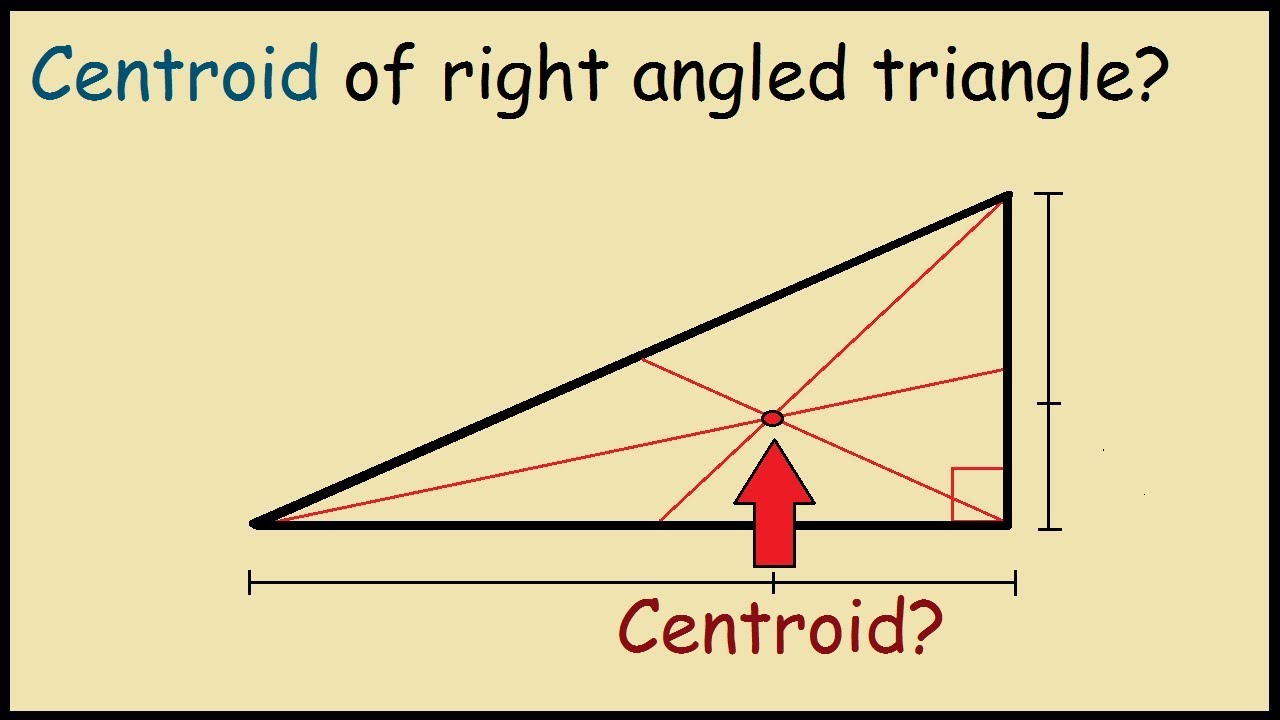
A median of a triangle is a line segment that joins a vertex to the midpoint of the side that is opposite to that vertex. The centroid of a triangle is the point at which the three medians intersect. It is referred to as the "center of mass" or "balance point" of the triangle. What is the centroid of an equilateral triangle? So if this distance right here is a, then this distance right here is 2a. Download Now. And remember, this point right over here-- this is the median of this bottom side right over here. Those lines are the medians. The centroid of a triangle can be found using the coordinates of the vertices of the given triangle. The centroid of a triangle always lies within the triangle.

The centroid of a triangle is a point of concurrency of the medians of a triangle. Before understanding the point of concurrency, let us discuss the medians of a triangle.

So CE must be 9 cm long. Flag Button navigates to signup page. Correct answer is: Both a and c are correct. A median of a triangle is a line segment that joins a vertex to the midpoint of the side that is opposite to that vertex. Median OF is 36 cm long. What Is the Centroid of a Triangle? Think: 7. Then the formula of the centroid of a triangle is given by. Let's see, the midpoint of the opposite side is there. AP Statistics Tutors near me. You will also be able to relate the centroid to the center of gravity, and calculate the length of medians using a triangle's centroid, and find the centroid using only one median. Let's just use this coordinate right here and then compare just using the distance formula. The formula for the centroid of the triangle is as follows:. Suppose PQR is a triangle having a centroid V.