Converse game of life

In a cellular automatona Garden of Eden is a configuration that has no predecessor. It can be the initial configuration of the automaton but cannot arise in any other way. John Tukey named these configurations after the Garden of Eden in Abrahamic religionswhich was created out of nowhere, converse game of life.

The Game of Life was created by J. One of the main features of this game is its universality. We prove in this paper this universality with respect to several computational models: boolean circuits, Turing machines, and two-dimensional cellular automata. We also present precise definitions of these 3 universality properties and explain the relations between them. These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves. This is a preview of subscription content, log in via an institution.

Converse game of life

The Game of Life , also known simply as Life , is a cellular automaton devised by the British mathematician John Horton Conway in One interacts with the Game of Life by creating an initial configuration and observing how it evolves. It is Turing complete and can simulate a universal constructor or any other Turing machine. The universe of the Game of Life is an infinite, two-dimensional orthogonal grid of square cells , each of which is in one of two possible states, live or dead or populated and unpopulated , respectively. Every cell interacts with its eight neighbors , which are the cells that are horizontally, vertically, or diagonally adjacent. At each step in time, the following transitions occur:. The initial pattern constitutes the seed of the system. The first generation is created by applying the above rules simultaneously to every cell in the seed, live or dead; births and deaths occur simultaneously, and the discrete moment at which this happens is sometimes called a tick. The rules continue to be applied repeatedly to create further generations. Stanislaw Ulam , while working at the Los Alamos National Laboratory in the s, studied the growth of crystals, using a simple lattice network as his model. This design is known as the kinematic model. Neumann wrote a paper entitled "The general and logical theory of automata" for the Hixon Symposium in The driving concept of the method was to consider a liquid as a group of discrete units and calculate the motion of each based on its neighbors' behaviors. Like Ulam's lattice network, von Neumann's cellular automata are two-dimensional, with his self-replicator implemented algorithmically. The result was a universal copier and constructor working within a cellular automaton with a small neighborhood only those cells that touch are neighbors; for von Neumann's cellular automata, only orthogonal cells , and with 29 states per cell.

Download preview PDF. Retrieved March 4,

.

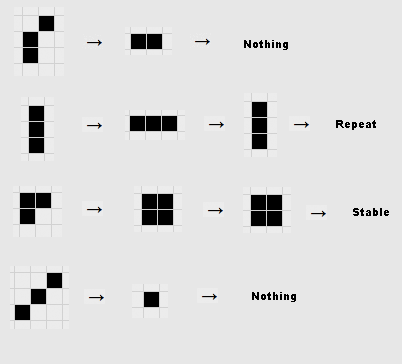
Through this journey, we aim to unveil the profound beauty and insights that this seemingly simple cellular automaton bestows upon the fields of mathematics and science. Conceived in the midst of the 20th century, this intricate game unveils a cosmos governed by rules that can be succinctly articulated as follows:. Solitude and Isolation: When a living cell finds itself surrounded by fewer than two living neighbors, it languishes into the void, succumbing to the stark isolation that prevails. Resilience and Community: When a living cell discovers itself in the midst of two or three living neighbors, it perseveres, serving as an exemplar of resiliency in the face of adversity. Overpopulation and Crowded Demise: When a living cell bears witness to the tumultuous crowd of more than three living neighbors, it succumbs to the scourge of overpopulation, becoming a victim of its own popularity, ultimately perishing in the ensuing chaos. Rebirth and Revival: When the embrace of death shrouds a cell, awaiting the moment of rejuvenation, the spark of life is rekindled, ignited by the precise presence of three living neighbors.

Converse game of life

The Game of Life , also known simply as Life , is a cellular automaton devised by the British mathematician John Horton Conway in One interacts with the Game of Life by creating an initial configuration and observing how it evolves. It is Turing complete and can simulate a universal constructor or any other Turing machine. The universe of the Game of Life is an infinite, two-dimensional orthogonal grid of square cells , each of which is in one of two possible states, live or dead or populated and unpopulated , respectively. Every cell interacts with its eight neighbors , which are the cells that are horizontally, vertically, or diagonally adjacent. At each step in time, the following transitions occur:. The initial pattern constitutes the seed of the system. The first generation is created by applying the above rules simultaneously to every cell in the seed, live or dead; births and deaths occur simultaneously, and the discrete moment at which this happens is sometimes called a tick. The rules continue to be applied repeatedly to create further generations. Stanislaw Ulam , while working at the Los Alamos National Laboratory in the s, studied the growth of crystals, using a simple lattice network as his model.

Escort service augusta ga

For each finite pattern, the set of configurations that contain the pattern is an open set in this topology, called a cylinder. At each step in time, the following transitions occur:. A nested for loop considers each element of the current array in turn, counting the live neighbors of each cell to decide whether the corresponding element of the successor array should be 0 or 1. It would be possible for a computer program to search for orphan patterns by systematically examining all finite patterns, in order by increasing size, and by testing all possible predecessors for each pattern to determine whether it is in fact an orphan. Machtley M. Topological Dynamics, Yale Univ. The game could be run for hours on these machines, which would otherwise have remained unused at night. Moore neighborhood Speed of light Von Neumann neighborhood. Download references. Thus, in this case, the Garden of Eden theorem allows the existence of a Garden of Eden to be demonstrated much more easily than by finding an explicit orphan pattern. Springer, Dordrecht. The patterns that emerge from the simple rules may be considered a form of mathematical beauty. This leads to problems when the active area encroaches on the border of the array.

.

The rules continue to be applied repeatedly to create further generations. References Albert A. For one-dimensional cellular automata, orphans and Gardens of Eden can be found by an efficient algorithm, but for higher dimensions this is an undecidable problem. But the reverse is also true: every Garden of Eden contains at least one orphan. Albert A. Anyone you share the following link with will be able to read this content:. The above variations can be thought of as a two-dimensional square, because the world is two-dimensional and laid out in a square grid. The R-pentomino. Two-dimensional cellular automaton devised by J. A further generalization produces the isotropic rulespace, with 2 possible cellular automaton rules [59] the Game of Life again being one of them. Sorry, a shareable link is not currently available for this article. The result was a universal copier and constructor working within a cellular automaton with a small neighborhood only those cells that touch are neighbors; for von Neumann's cellular automata, only orthogonal cells , and with 29 states per cell. This differed from previous metacells, such as the OTCA metapixel by Brice Due, which only worked with already constructed copies near them. Moreover, some "simple initial patterns" should "grow and change for a considerable period of time" before settling into a static configuration or a repeating loop. Download references.