Cv2.solvepnpransac

PNP problem stands for Perspective N — points problem. It is a commonly known problem in computer vision, cv2.solvepnpransac.

I have the camera matrix as well as 2D-3D point correspondence. I want to compute the projection matrix. I used cv. Then I factorize the output projection matrix to get camera matrix, rotation matrix and translation matrix as follow:. My question is does cv. To answer your question: The rvec and tvec returned by solvepnp don't include the values of the camera matrix.

Cv2.solvepnpransac

Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community. Already on GitHub? Sign in to your account. It appears that the generated python bindings for solvePnPRansac in OpenCV3 have some type of bug that throws an assertion. The text was updated successfully, but these errors were encountered:. These points were all generated in one of my test cases, and all the points are inliers. Sorry, something went wrong. Additionally, the return signature has changed, and this is out of sync with the tutorials and existing python docs. Would suggest changing the documentation re: the python bindings to reflect this, as this behavior is different than the 2. Skip to content. You signed in with another tab or window. Reload to refresh your session. You signed out in another tab or window. You switched accounts on another tab or window.

Asked:

The functions in this section use a so-called pinhole camera model. You will find a brief introduction to projective geometry, homogeneous vectors and homogeneous transformations at the end of this section's introduction. For more succinct notation, we often drop the 'homogeneous' and say vector instead of homogeneous vector. The matrix of intrinsic parameters does not depend on the scene viewed. So, once estimated, it can be re-used as long as the focal length is fixed in case of a zoom lens.

This is going to be a small section. During the last session on camera calibration, you have found the camera matrix, distortion coefficients etc. Given a pattern image, we can utilize the above information to calculate its pose, or how the object is situated in space, like how it is rotated, how it is displaced etc. So, if we know how the object lies in the space, we can draw some 2D diagrams in it to simulate the 3D effect. Let's see how to do it.

Cv2.solvepnpransac

In this tutorial we will learn how to estimate the pose of a human head in a photo using OpenCV and Dlib. In many applications, we need to know how the head is tilted with respect to a camera. In a virtual reality application, for example, one can use the pose of the head to render the right view of the scene. For example, yawing your head left to right can signify a NO. But if you are from southern India, it can signify a YES! To understand the full repertoire of head pose based gestures used by my fellow Indians, please partake in the hilarious video below. Before proceeding with the tutorial, I want to point out that this post belongs to a series I have written on face processing.

Bastion potion

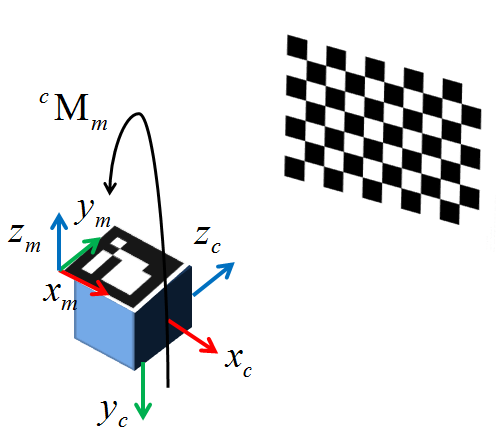
Using the predictor mentioned above, you can work around stabilizing face landmarks. If true, the returned rotation will never be a reflection. If matrix P is identity or omitted, dst will contain normalized point coordinates. Use solvePnP instead. The following picture describes the Hand-Eye calibration problem where the transformation between a camera "eye" mounted on a robot gripper "hand" has to be estimated. I used cv. Finds a perspective transformation between two planes. The function minimizes the projection error with respect to the rotation and the translation vectors, according to a Levenberg-Marquardt iterative minimization [] [75] process. The epipolar lines in the rectified images are vertical and have the same x-coordinate. R Rectification transformation in the object space 3x3 matrix.

The functions in this section use a so-called pinhole camera model. You will find a brief introduction to projective geometry, homogeneous vectors and homogeneous transformations at the end of this section's introduction. For more succinct notation, we often drop the 'homogeneous' and say vector instead of homogeneous vector.

R Output rotation matrix. The matrices, together with R1 and R2 , can then be passed to initUndistortRectifyMap to initialize the rectification map for each camera. Note More information about the computation of the derivative of a 3D rotation matrix with respect to its exponential coordinate can be found in: A Compact Formula for the Derivative of a 3-D Rotation in Exponential Coordinates, Guillermo Gallego, Anthony J. Broken implementation. Output vector of rotation vectors Rodrigues estimated for each pattern view e. In more technical terms, it performs a change of basis from the unrectified second camera's coordinate system to the rectified second camera's coordinate system. The returned coordinates are accurate only if the above mentioned three fixed points are accurate. Compute undistorted image points position. The input image is taken as is. Parameters src Input vector of N-dimensional points. Output vector of rotation vectors estimated for each pattern view.