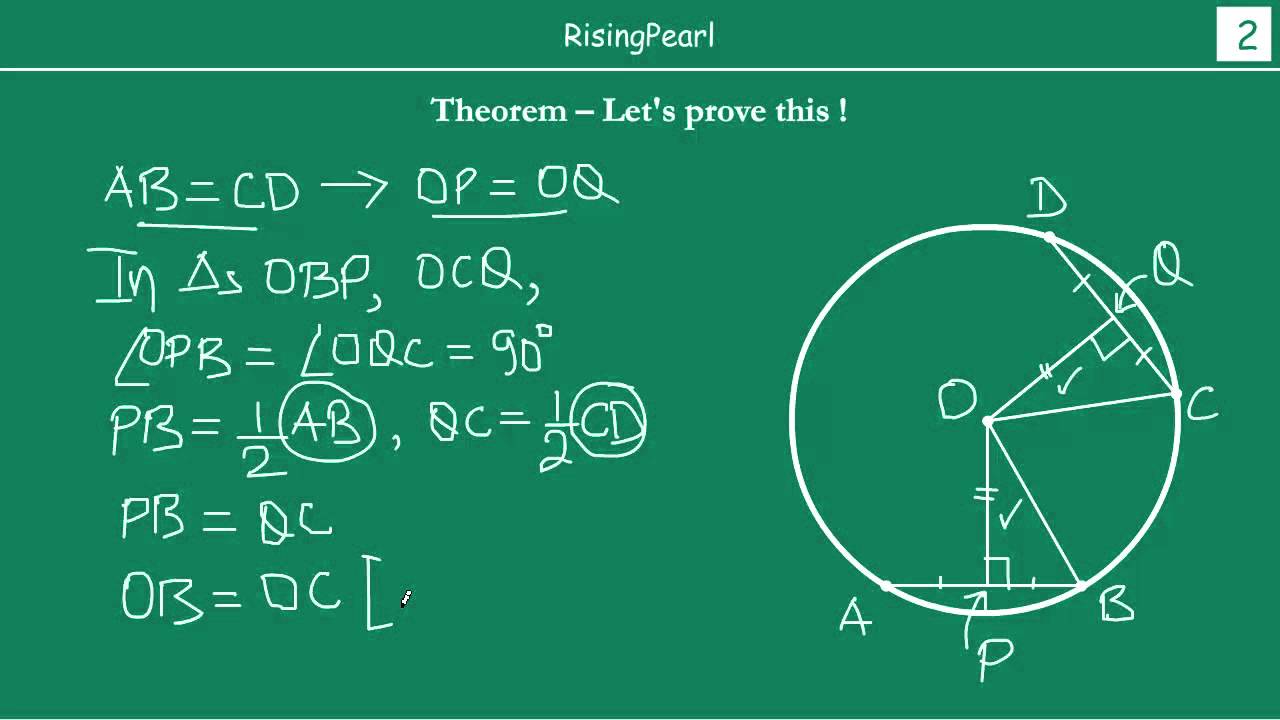
Equal chords are equidistant from the centre

In the realm of Mathematics, a chord can be described as a line segment that connects two points on a circle's circumference. Interestingly, a circle can have an infinite number of chords.

In Mathematics, a chord is the line segment which joins two points on the circumference of a circle. In general, a circle can have infinitely many chords. The distance of the line from a point is defined as the perpendicular distance from a point to a line. If you draw infinite chords to a circle, the longer chord is close to the centre of the circle, than the smaller chord of a circle. In this article, we will discuss the theorem and proof related to the equal chords and their distance from the centre and also its converse theorem in detail.

Equal chords are equidistant from the centre

Last updated at March 8, by Teachoo. Learn in your speed, with individual attention - Teachoo Maths 1-on-1 Class. Theorem 9. Given : A circle with center at O. AB and CD are two equal chords of circle i. Davneet Singh has done his B. Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 14 years. Your browser does not support the audio element. Maths Classes. Old search 1.

Report An Error.

Well, we see many round objects in daily life like coins, clocks, wheels, bangles, and many more. In this article, we will learn about the equal chords theorem i. And then will learn its converse too. After that, we discussed the theorem regarding the intersection of equal chords. At last, we will learn the diameter is the largest chord of the circle and we will solve examples to understand the concepts more easily. Perpendicular Bisector of the Chord. Here, two points are joined to form a line segment which we call as Chord of the circle.

In Mathematics, a chord is the line segment which joins two points on the circumference of a circle. In general, a circle can have infinitely many chords. The distance of the line from a point is defined as the perpendicular distance from a point to a line. If you draw infinite chords to a circle, the longer chord is close to the centre of the circle, than the smaller chord of a circle. In this article, we will discuss the theorem and proof related to the equal chords and their distance from the centre and also its converse theorem in detail.

Equal chords are equidistant from the centre

If XY is 10, what is the length of AB? We can use the good old pythagorean theorem. The blue line on the left is perpendicular to the two chords. The radius of the circle is How large is X?

Call budget rental

In this article, we will discuss the theorem and proof related to the equal chords and their distance from the centre and also its converse theorem in detail. AB and CD are chords that are equal i. Now, we will see the proof:. Therefore, the chords AB and CD are equal. Two equal chords of a circle intersect within the circle. As we can see, line ON is perpendicular to AB and it has the shortest length i. View Test Series. Tech from Indian Institute of Technology, Kanpur. Table Of So, for the chord AB:. Also, read : Circumference of a Circle Congruence of Triangles. Book a free demo. The distance of a line from a point is typically determined by the perpendicular distance from that point to the line. As the perpendicular from the centre of the circle to a chord, bisects the chord, we can write it as.

In the realm of Mathematics, a chord can be described as a line segment that connects two points on a circle's circumference. Interestingly, a circle can have an infinite number of chords.

Exploring Equal Chords and their Distance from the Centre: Theorem and Proof Theorem: Equal chords in a circle or congruent circles have equal distances from the centre or centres. Then, draw a line OM from the center to the chord AB. Perpendicular Bisector of the Chord. The distance of the line from a point is defined as the perpendicular distance from a point to a line. Therefore, the chords AB and CD are equal. Find the lengths of OS and OT. Chapter 9 Class 9 Circles Serial order wise Theorems. This article delves into the theorem and proof concerning equal chords and their distance from the centre, as well as its converse theorem. As the perpendicular from the centre of the circle to a chord, bisects the chord, we can write it as. Please login :. Root Finder. The article summarizes the theorem of equal chords and their distances from the center i.