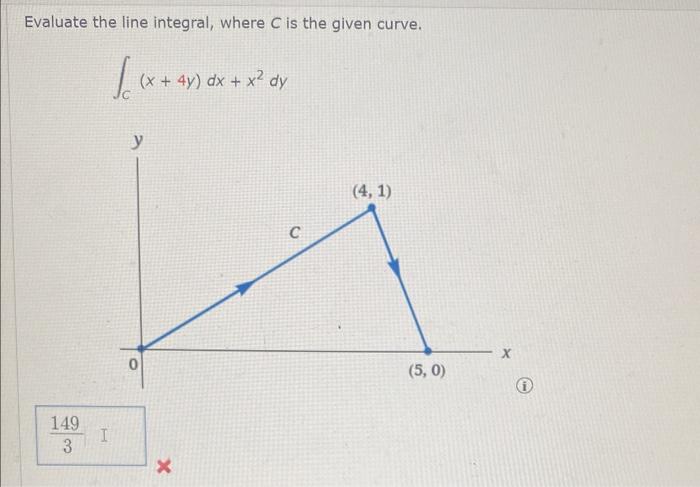
Evaluate the line integral where c is the given curve

In the previous two sections we looked at line integrals of functions. In this section we are going to evaluate line integrals of vector fields.

Evaluate the line integral, where C is the given curve. Use a calculator or CAS to evaluate the line integral correct to four decimal places. Short Answer Step-by-step Solution. Now share some education! Short Answer Expert verified.

Evaluate the line integral where c is the given curve

We have so far integrated "over'' intervals, areas, and volumes with single, double, and triple integrals. We now investigate integration over or "along'' a curve—"line integrals'' are really "curve integrals''. As with other integrals, a geometric example may be easiest to understand. What is the area of the surface thus formed? We already know one way to compute surface area, but here we take a different approach that is more useful for the problems to come. As usual, we start by thinking about how to approximate the area. We pick some points along the part of the parabola we're interested in, and connect adjacent points by straight lines; when the points are close together, the length of each line segment will be close to the length along the parabola. If we add up the areas of these rectangles, we get an approximation to the desired area, and in the limit this sum turns into an integral. Then as we have seen in section Example Now we turn to a perhaps more interesting example. Recall that in the simplest case, the work done by a force on an object is equal to the magnitude of the force times the distance the object moves; this assumes that the force is constant and in the direction of motion. We have already dealt with examples in which the force is not constant; now we are prepared to examine what happens when the force is not parallel to the direction of motion. We have already examined the idea of components of force, in example In other words, work is computed using a particular line integral of the form we have considered.

As we shrink the arc lengths to zero, their values become close enough that any small difference becomes irrelevant. In this case, Equation 6. Power Series 9.

Such an interval can be thought of as a curve in the xy -plane, since the interval defines a line segment with endpoints a , 0 a , 0 and b , 0 b , 0 —in other words, a line segment located on the x -axis. Suppose we want to integrate over any curve in the plane, not just over a line segment on the x -axis. Such a task requires a new kind of integral, called a line integral. Line integrals have many applications to engineering and physics. They also allow us to make several useful generalizations of the Fundamental Theorem of Calculus. And, they are closely connected to the properties of vector fields, as we shall see.

Such a task requires a new kind of integral, called a line integral. Line integrals have many applications to engineering and physics. They also allow us to make several useful generalizations of the Fundamental Theorem of Calculus. And, they are closely connected to the properties of vector fields, as we shall see. A line integral gives us the ability to integrate multivariable functions and vector fields over arbitrary curves in a plane or in space.

Evaluate the line integral where c is the given curve

In this section we are now going to introduce a new kind of integral. However, before we do that it is important to note that you will need to remember how to parameterize equations, or put another way, you will need to be able to write down a set of parametric equations for a given curve. You should have seen some of this in your Calculus II course. If you need some review you should go back and review some of the basics of parametric equations and curves. In fact, we will be using the two-dimensional version of this in this section.

Vintage pumpkin planter

Example With scalar line integrals, neither the orientation nor the parameterization of the curve matters. Across all devices. However, there is no reason to restrict ourselves like that. Lagrange Multipliers 15 Multiple Integration 1. Notice that this is the negative of the answer in Example 6. Using this notation, the line integral becomes,. This website uses cookies to improve your experience. The distance between two points along a curve is known as arc length. Alternatively, if a curve on a map represents a road, we might want to know how far we need to drive to get to our destination. In Combinatorial Optimization 24 Data Analysis.

To illustrate the idea, think about how it feels to run on a track on a windy day or to row a boat across a lake with a noticeable current? The path of the wind or the flow of the current might make it easier in one direction than the other, right?

Here is the parameterization of the curve. Change of Variables 16 Vector Calculus 1. Q: Evaluate the line integral along the given paths. Due to the nature of the mathematics on this site it is best views in landscape mode. We can do this because all the points in the curve are in the domain of f. We chop the curve into small pieces. To see where the term circulation comes from and what it measures, let v represent the velocity field of a fluid and let C be an oriented closed curve. A thin wire is bent into the shape of a semicircle of radius a. A: C consist line from A 2, 0, 1 to B 3, 3, 1 Now,. Any cookies that may not be particularly necessary for the website to function and is used specifically to collect user personal data via analytics, ads, other embedded contents are termed as non-necessary cookies. Here is a parameterization for this curve. Line integrals have many applications to engineering and physics. Q: Find the line integral of x ds over C where c is the line segment from 1,0 to 0,1 using two…. Here i…. Exterior Angle Theorem.