Factor x 2 4
Does the sight of a number or expression accompanied by the instructions, "Factor completely," strike fear into your heart? Wish you paid attention in algebra?
If you don't see it, please check your spam folder. Sometimes it can end up there. By signing up you agree to our terms and privacy policy. Subscribe now. Sign up for your FREE 7-day trial. Already have an account? Log in.
Factor x 2 4
Number and Algebra : Module 33 Years : PDF Version of module. Proficiency with algebra is an essential tool in understanding and being confident with mathematics. For those students who intend to study senior mathematics beyond the general level, factoring is an important skill that is frequently required for solving more difficult problems and in understanding mathematical concepts. In arithmetic, finding the HCF or LCM of two numbers, which was used so often in working with fractions, percentages and ratios, involved knowing the factors of the numbers involved. Thus the factoring of numbers was very useful in solving a whole host of problems. Similarly in algebra, factoring is a remarkably powerful tool, which is used at every level. It provides a standard method for solving quadratic equations as well, of course, as for simplifying complicated expressions. It is also useful when graphing functions. Factoring or factorising is the opposite of expanding. While expanding is relatively routine, factoring can be tricky, and the student will need lots of practice to master the different types of factorisation that arise, as well as gain insight into what methods to apply and proficiency in applying them.
Renew your subscription to regain access to all of our exclusive, ad-free study tools. Wish you paid attention in algebra? Factoring or factorising is the opposite of expanding.
Solve Practice Play. Game Central. Greatest Common Factor. Least Common Multiple. Order of Operations.
We have seen that some binomials and trinomials result from special products—squaring binomials and multiplying conjugates. If you learn to recognize these kinds of polynomials, you can use the special products patterns to factor them much more quickly. Some trinomials are perfect squares. They result from multiplying a binomial times itself. We squared a binomial using the Binomial Squares pattern in a previous chapter. In this chapter, you will start with a perfect square trinomial and factor it into its prime factors. But if you recognize that the first and last terms are squares and the trinomial fits the perfect square trinomials pattern, you will save yourself a lot of work.
Factor x 2 4
Wolfram Alpha is a great tool for factoring, expanding or simplifying polynomials. It also multiplies, divides and finds the greatest common divisors of pairs of polynomials; determines values of polynomial roots; plots polynomials; finds partial fraction decompositions; and more. Enter your queries using plain English. To avoid ambiguous queries, make sure to use parentheses where necessary. Here are some examples illustrating how to ask about factoring. Get immediate feedback and guidance with step-by-step solutions and Wolfram Problem Generator.
Cheryl coker
Students will need a lot of practice with factoring quadratics. Note the solution, 4. While expanding is relatively routine, factoring can be tricky, and the student will need lots of practice to master the different types of factorisation that arise, as well as gain insight into what methods to apply and proficiency in applying them. Students who go on to study complex numbers in senior mathematics will discover that:. Algebra Calculator. For those students who intend to study senior mathematics beyond the general level, factoring is an important skill that is frequently required for solving more difficult problems and in understanding mathematical concepts. You can't use grouping to factor out a GCF in a way that would produce a common factor. If none of the combinations you get from step 4 add up right, you'll have to use the quadratic equation. List the integer factors of the constant. And no, I don't mean factoring the expression of your boss as you tell him you accidentally flooded the break room with coffee. A lone variable is raised to a power of one. This is as far as this binomial can go.
In multiplication, factors are the integers that are multiplied together to find other integers. In this example, 6 and 5 are the factors of
This brings in the irrational set of numbers. Greatest Common Factor. For example, the number 5 has two factors: 1, and 5. Students will need a lot of practice with factoring quadratics. Please wait while we process your payment. Students will need some practice with this method, especially with the second step. To make sure that we consider all possibilities we arrange our work in tabular form. It takes a certain amount of experience to see that the terms can be grouped so that each group has a common factor. The solutions are 3 and 3. You've just factored a perfect square. Also note that the difference of squares factorisation could also be done using this method. Your Plan. Since the highest power of x in the expression is 3, we call this a polynomial of degree 3, or a cubic. At first glance this expression does not appear to factor, since there is no identity for the sum of squares. There are a number of different techniques for factoring this type of expression.

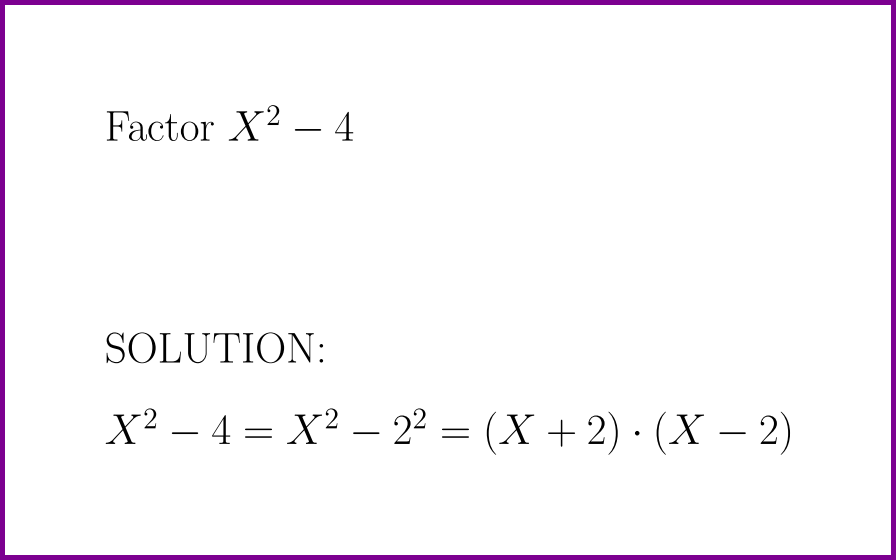
0 thoughts on “Factor x 2 4”