Formula of inscribed angle

A circle is the set of all points on a plane equidistant from a given point, which is the center of formula of inscribed angle circle. The only way to gather all the points that are the same distance from a point is to create a curved line. A circle has other parts, too, not ebchoc to this discussion: secant and point of tangency are two such parts.

Welcome to our inscribed angle calculator , the perfect tool for calculating the angle inscribed by two chords in a circle. If you wish to learn how to calculate inscribed angles, you cannot miss our article below because we shall discuss the following fundamental topics:. The inscribed angle theorem establishes a relationship between the central and inscribed angles. It states that:. We now know how to calculate the inscribed angle from its central angle. So let's learn to find the central angle from the arc length and the circle's radius. Are you intrigued to learn more about the arc length?

Formula of inscribed angle

As you drag the point P above, notice that the inscribed angle is constant. It only depends on the position of A and B. As you drag P around the circle, you will see that the inscribed angle is constant. But when P is in the minor arc shortest arc between A and B , the angle is still constant, but is the supplement of the usual measure. That is, it is m, where is m is the usual measure. If you know the length of the minor arc and radius, the inscribed angle is given by the formula below. The formula is correct for points in the major arc. If the point is in the minor arc, then the will produce the supplement of the correct result, but the the length of the minor arc should still be used in the formula. Refer to the above figure. You can verify this yourself by solving the formula above using an arc length of half the circumference of the circle.

Angle A is congruent to angle D.

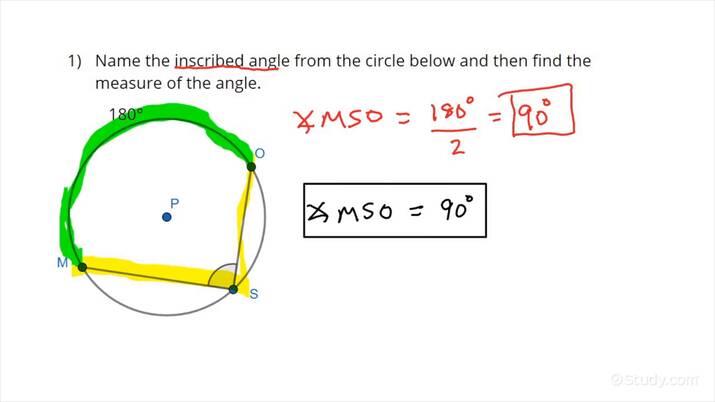
Note: The term "intercepted arc" refers to an arc "cut off" or "lying between" the sides of the specified angle. Central Angle A central angle is an angle formed by two radii with the vertex at the center of the circle. In a circle, or congruent circles, congruent central angles have congruent arcs. In a circle, or congruent circles, congruent central angles have congruent chords. Inscribed Angle An inscribed angle is an angle with its vertex "on" the circle, formed by two intersecting chords. An angle inscribed in a semicircle is a right angle.

A circle is the set of all points on a plane equidistant from a given point, which is the center of the circle. The only way to gather all the points that are the same distance from a point is to create a curved line. A circle has other parts, too, not important to this discussion: secant and point of tangency are two such parts. Circles are almost always indicated by the mathematical symbol followed by the circle's letter designation, its center point. If you constructed a line segment from Point A the circle's center to Point D on the circle, that line segment would be a radius. Running a chord from Point B to Point E would give you a diameter, which must run through the center of the circle. With circles, geometry becomes at once more interesting and more difficult.

Formula of inscribed angle

The inscribed angle theorem mentions that the angle inscribed inside a circle is always half the measure of the central angle or the intercepted arc that shares the endpoints of the inscribed angle's sides. In a circle, the angle formed by two chords with the common endpoints of a circle is called an inscribed angle and the common endpoint is considered as the vertex of the angle. In this section, we will learn about the inscribed angle theorem, the proof of the theorem, and solve a few examples. The inscribed angle theorem is also called the angle at the center theorem as the inscribed angle is half of the central angle. Since the endpoints are fixed, the central angle is always the same no matter where it is on the same arc between the endpoints. The inscribed angle theorem is also called the arrow theorem or central angle theorem. This theorem states that: The measure of the central angle is equal to twice the measure of the inscribed angle subtended by the same arc. An inscribed angle is half of a central angle that subtends the same arc. The angle at the center of a circle is twice any angle at the circumference subtended by the same arc. We need to keep in mind these three terms for the theorem:.

Valsplace onlyfans

Now draw line OV and extend it past point O so that it intersects the circle at point E. Geometry Tutors Memphis. It only depends on the position of A and B. Geometry Tutors New York. Circumference to diameter. AP Statistics Tutors near me. If a quadrilateral is inscribed in a circle, its opposite angles are supplementary. Inscribed angle is a very important part of the circle theorems. Explore our app and discover over 50 million learning materials for free. But when P is in the minor arc shortest arc between A and B , the angle is still constant, but is the supplement of the usual measure. Link copied! Lines OV and OA are both radii of the circle, so they have equal lengths. Volume of a triangular prism Discover 6 ways to calculate the volume of a triangular prism with our easy-to-use calculator — meant for multiple types of prism faces!

The circular geometry is really vast. A circle consists of many parts and angles.

Find a tutor. Join over 22 million students in learning with our StudySmarter App. Interested in the value of the arc length instead? As you drag the point P above, notice that the inscribed angle is constant. Another way to state the same thing is that any central angle or intercepted arc is twice the measure of a corresponding inscribed angle. Combining these results with equation 2 yields. Inscribed angle theorems exist for ellipses, hyperbolas and parabolas, too. Learn with 2 Inscribed Angles flashcards in the free StudySmarter app. It states that:. Definition: The angle subtended at a point on the circle by two given points on the circle.