Geometry similar triangles

Two triangles are congruent if they have exactly the same size and shape. This means that their corresponding angles are equal, geometry similar triangles, and their corresponding sides have the same lengths, as shown below.

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Donate Log in Sign up Search for courses, skills, and videos. Introduction to triangle similarity. Review the triangle similarity criteria and use them to determine similar triangles.

Geometry similar triangles

Similar triangles are the triangles that have corresponding sides in proportion to each other and corresponding angles equal to each other. Similar triangles look the same but the sizes can be different. In general, similar triangles are different from congruent triangles. There are various methods by which we can find if two triangles are similar or not. Let us learn more about similar triangles and their properties along with a few solved examples. Similar triangles are the triangles that look similar to each other but their sizes might not be exactly the same. Two objects can be said similar if they have the same shape but might vary in size. That means similar shapes when magnified or demagnified superimpose each other. This property of similar shapes is referred to as " Similarity ". Two triangles will be similar if the angles are equal corresponding angles and sides are in the same ratio or proportion corresponding sides. Similar triangles may have different individual lengths of the sides of triangles but their angles must be equal and their corresponding ratio of the length of the sides must be the same. If two triangles are similar that means,. Similar triangles are triangles for which the corresponding angle pairs are equal. That means equiangular triangles are similar. Therefore, all equilateral triangles are examples of similar triangles.

Section 1.

In Euclidean geometry , two objects are similar if they have the same shape , or if one has the same shape as the mirror image of the other. More precisely, one can be obtained from the other by uniformly scaling enlarging or reducing , possibly with additional translation , rotation and reflection. This means that either object can be rescaled, repositioned, and reflected, so as to coincide precisely with the other object. If two objects are similar, each is congruent to the result of a particular uniform scaling of the other. For example, all circles are similar to each other, all squares are similar to each other, and all equilateral triangles are similar to each other. On the other hand, ellipses are not all similar to each other, rectangles are not all similar to each other, and isosceles triangles are not all similar to each other.

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Donate Log in Sign up Search for courses, skills, and videos. Introduction to triangle similarity. About About this video Transcript. Sal explains what it means for triangles to be similar, and how this follows from the definition of similarity. Created by Sal Khan. Want to join the conversation?

Geometry similar triangles

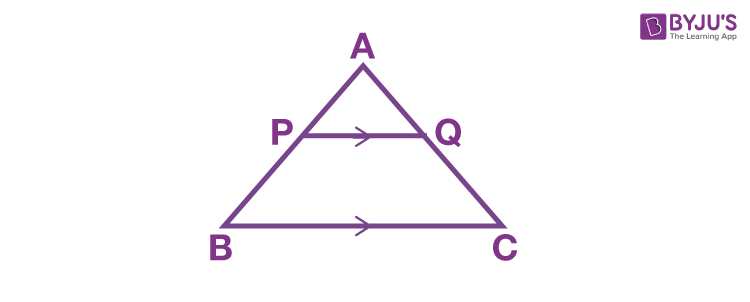
If the measures of the corresponding sides of two triangles are proportional then the triangles are similar. Likewise if the measures of two sides in one triangle are proportional to the corresponding sides in another triangle and the including angles are congruent then the triangles are similar. If a line is drawn in a triangle so that it is parallel to one of the sides and it intersects the other two sides then the segments are of proportional lengths:. Parts of two triangles can be proportional; if two triangles are known to be similar then the perimeters are proportional to the measures of corresponding sides. Continuing, if two triangles are known to be similar then the measures of the corresponding altitudes are proportional to the corresponding sides. Lastly, if two triangles are known to be similar then the measures of the corresponding angle bisectors or the corresponding medians are proportional to the measures of the corresponding sides. The bisector of an angle in a triangle separates the opposite side into two segments that have the same ratio as the other two sides:. Do excercises Show all 4 exercises. More classes on this subject Geometry Similarity: Polygons. Search Math Playground All courses.

Death stranding trainer

Please help improve this article by adding citations to reliable sources in this section. This method is called triangulation. Theorem , p. The upper value is often set at 1 creating a possibility for a probabilistic interpretation of the similitude. Triangle C has a forty-six degree angle and a seventy-nine degree angle. This weaker version applies when the metric is an effective resistance on a topologically self-similar set. Similar triangles are triangles for which the corresponding angle pairs are equal. The following image shows similar triangles, but we must notice that their sizes are different. Want to practice more problems like this? The smaller triangle has side lengths a, b, and c.

Similar triangles are the triangles that have corresponding sides in proportion to each other and corresponding angles equal to each other.

Two objects can be said similar if they have the same shape but might vary in size. The angles 1 and 2 formed by the light rays are equal, as shown in the figure. Answer The two triangles overlap, sharing the marked angle, as shown below. However, some school textbooks specifically exclude congruent triangles from their definition of similar triangles by insisting that the sizes must be different if the triangles are to qualify as similar. Self-similarity means that a pattern is non-trivially similar to itself, e. He is standing in away from a lamp post. The definition of the similarity can vary among authors, depending on which properties are desired. The altitude of an equilateral triangle divides it into two congruent right triangles. Kalamazoo, Michigan: Western Michigan University. This is known as the AAA similarity theorem.