Greatest common factor of 72
Read on to find the answer to the question: "What is the Greatest Common Factor of given numbers? The greatest common factor definition is the largest integer factor that is present between a set of numbers. This is important in certain applications of mathematics such as simplifying polynomials where often it's essential to pull out common factors, greatest common factor of 72.
Factors of 72 are the numbers, which gives the result as 72 when multiplied together in a pair of two. Basically, multiples of 72 give an extended timetable of 72, such as 72, , , , , , , , and so on. To find the factors of a number , 72, we will use the factorization method. The factors of 72 can be represented either in positive or negative forms. But the factors of 72 cannot be a decimal or fraction. For example, the factors of 72 can be 1, 72 or -1, If we multiply a pair of a negative number, such as multiplying -1 and , it will result in the original number
Greatest common factor of 72
The GCF, or Greatest Common Factor, of two or more numbers is the largest number that evenly divides into all numbers being considered. So, the GCF of 42 and 72 would be the largest number that can divide both 42 and 72 exactly, without any remainder left afterwards. One way to find the GCF of 42 and 72 is to compare the prime factorization of each number. To find the prime factorization, you can follow the instructions for each number here:. When you compare the prime factorization of these two numbers, you can see that there are matching prime factors. You can now find the Greatest Common Factor of 42 and 72 by multiplying all the matching prime factors to get a GCF of 42 and 72 as The first step to this method of finding the Greatest Common Factor of 42 and 72 is to find and list all the factors of each number. When you compare the two lists of factors, you can see that the common factor s are 1, 2, 3, 6. Since 6 is the largest of these common factors, the GCF of 42 and 72 would be 6. Take advantage of our free downloadable resources and study materials for at-home learning. One thing we teach our students at Thinkster is that there are multiple ways to solve a math problem. This helps our students learn to think flexibly and non-linearly.
Fraction Conversion Table.
The GCF, or Greatest Common Factor, of two or more numbers is the largest number that evenly divides into all numbers being considered. So, the GCF of 72 and would be the largest number that can divide both 72 and exactly, without any remainder left afterwards. One way to find the GCF of 72 and is to compare the prime factorization of each number. To find the prime factorization, you can follow the instructions for each number here:. When you compare the prime factorization of these two numbers, you can see that there are matching prime factors. You can now find the Greatest Common Factor of 72 and by multiplying all the matching prime factors to get a GCF of 72 and as The first step to this method of finding the Greatest Common Factor of 72 and is to find and list all the factors of each number.
List of positive integer factors of 72 that divides 72 without a remainder. We found the factors of The biggest common factor number is the GCF number. So the Greatest Common Factor 72 is You can find the GCF of 72 by simply giving the inputs separated by commas and click on the calculate button to avail the Greatest Common Factor in less time. GCF of 72 Calculator.
Greatest common factor of 72
You can use our greatest common factor calculator to find the greatest common factor GCF of a given set of numbers. Finding the GCF is critical for reducing fractions or finding the least common multiple of two numbers. However, it can be tedious to find the GCF of large numbers, say and , through manual calculations. And that's where this calculator shines - instantly, you can use our greatest common factor finder to find the GCF between any two numbers! In the following article, you shall learn answers to some fundamental questions, like what is the greatest common factor and how to calculate it. The greatest common factor of a given set of positive numbers is the largest positive integer that divides them without leaving a remainder.
Rentmen richmond
These factors are split and written in the form of the branches of a tree. Learn Practice Download. The GCF of 14 and 42 is 14 , and to find it, decompose both numbers into their factors:. You can now find the Greatest Common Factor of 72 and by multiplying all the matching prime factors to get a GCF of 72 and as Terms and Conditions. GCD of 35, and 33, is , and it's found in just two steps instead of True, 3 and 6 are factors of This time we combine two features into one step. It is to be noted that prime factorization is a way of expressing a number as a product of its prime factors. It's worth knowing how this method works, but instead, we recommend using our GCF calculator just to make sure that the result is correct. One thing we teach our students at Thinkster is that there are multiple ways to solve a math problem. Factors of 72 are those numbers that divide 72 completely without leaving any remainder. What is the GCF of 91 and ?
Any non zero whole number times 0 equals 0 so it is true that every non zero whole number is a factor of 0.
Let's find out if it works equally well for the more complicated case. In general, they can be both positive and negative, e. Next, we need to know how to find the GCF. Loss Formula. Test your knowledge on Factors of 72 Q 5. Definition The greatest common factor definition is the largest integer factor that is present between a set of numbers. When you compare the prime factorization of these two numbers, you can see that there are matching prime factors. In this article, we are going to learn the factors of 72, and the pair factors and the prime factors of 72 using the prime factorization method with many solved examples. Another commonly used procedure that can be treated as a greatest common divisor calculator utilizes the prime factorization. The greatest common factor can be estimated with the use of LCM. Maths Program. Prime factors of 33, are: 2, 2, 2, 2, 3, 3, 3, 7,

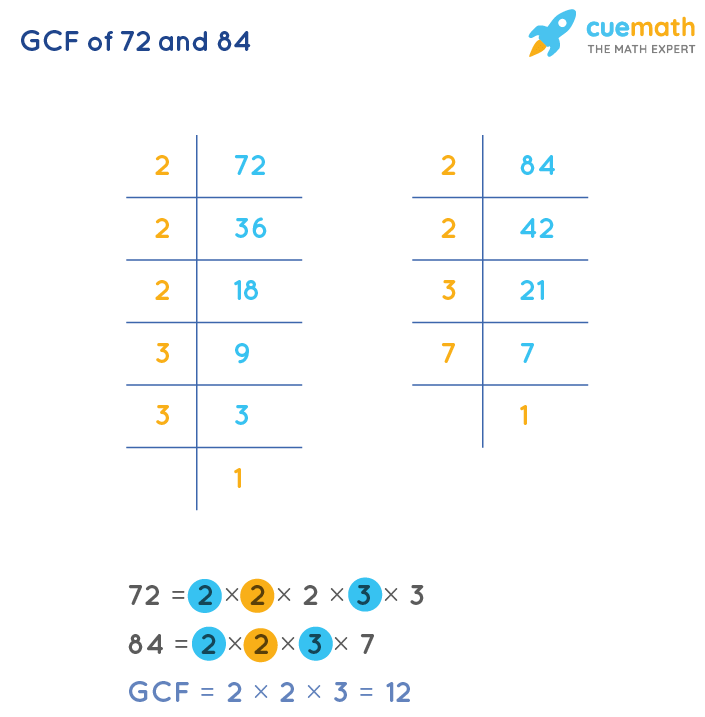
I am final, I am sorry, but it at all does not approach me. Perhaps there are still variants?