Interior and exterior angles of polygons worksheet

Exterior angles are angles between a polygon and the extended line from the vertex of the polygon. Check out our lessons on interior angles of polygons and sum of the interior angles to find out more. Includes reasoning and applied questions. Exterior angles of a polygon is part of our series of lessons to support revision on angles in polygons.

Here we will learn about angles in polygons including how to calculate angles in polygons using a variety of methods and an overview of interior and exterior angles. Angles in polygons relate to the interior and exterior angles of regular and irregular polygons. Interior angles are the angles within a polygon made by two sides. Step-by-step guide: Interior angles of a polygon. Exterior angles are the angles between a polygon and the extended line from the next side. Step-by-step guide: Exterior angles of a polygon. A polygon is a two dimensional shape with at least three sides, where the sides are all straight lines.

Interior and exterior angles of polygons worksheet

.

Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors. The size of each interior angle of a regular polygon is 11 times the size of each exterior angle.

.

What is the sum of the exterior angles of an octagon? What is the measure of one exterior angle of a regular decagon ten-sided polygon? What is the measure of each interior angle of a regular nonagon nine-sided polygon? How many sides does it have? One interior angle of a regular polygon is The given decagon is a regular polygon. So, all its exterior angles are of same measure. Because decagon is a ten-sided polygon, the measure of each exterior angle is. The given nonagon is a regular polygon.

Interior and exterior angles of polygons worksheet

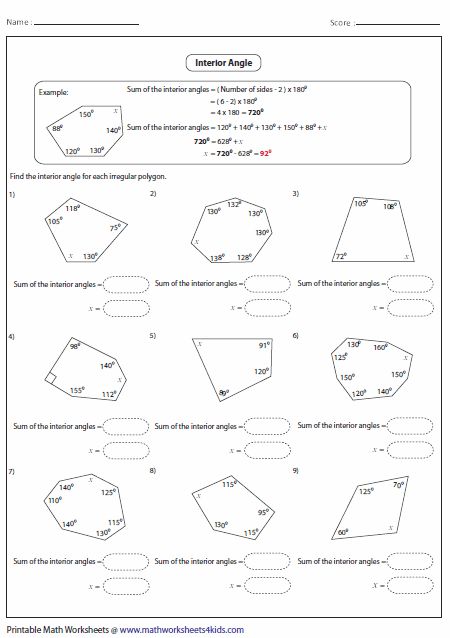
This assemblage of printable angles in polygons worksheets for grade 6 through high school encompasses a multitude of exercises to find the sum of interior angles of both regular and irregular polygons, find the measure of each interior and exterior angle, simplify algebraic expressions to find the angle measure and much more. Based on the number of sides used, these worksheets are categorized into easy and moderate levels of difficulty. Employ the Regular polygons - Angles chart as a precursor.

Homebodii reviews

How to find the sum of the interior angles of a polygon. Note whether these are regular or irregular shapes. We need to find the number of sides. This polygon is regular as all the sides are of equal length and the angles are of equal size. Next lessons. A 12 sided polygon can be divided into 10 triangles, and ten lots of is These cookies will be stored in your browser only with your consent. Other lessons in this series include:. This category only includes cookies that ensures basic functionalities and security features of the website. Example 4: complex polygon Identify how many sides the polygon has. Find out more about our GCSE maths tuition programme.

.

This topic is relevant for:. How to find the sum of the interior angles for a polygon. Step-by-step guide: Angles in a quadrilateral Using our knowledge of triangles we can find the sum of the interior angles of any polygon by splitting it into triangles. The sum of the interior angles of a polygon depends on how many sides it has, not what it looks like. A regular pentagon? Regular polygons have all angles are that are equal in size and all sides that are equal in length. In order to access this I need to be confident with: 2D shapes Types of angles Angles on a straight line Angles in a triangle. Step-by-step guide: Angles in a triangle Sum of the angles in a quadrilateral : A quadrilateral is a four sided shape. Note whether these are regular or irregular shapes. Or even an irregular octagon? These cookies do not store any personal information. You will be familiar with many types of polygons such as triangle, rectangle and pentagon. Despite these two decagons 10 sided shapes looking very different, the sum of their interior angles is the same. To work out the number of triangles a polygon can be split into we subtract 2 from the number of sides it has.