Lim sup
One possibility is to try and extract a convergent subsequence, as described in the last section.
As is the case with sequences of other objects, convergence is not necessary or even usual. More generally, again analogous to real-valued sequences, the less restrictive limit infimum and limit supremum of a set sequence always exist and can be used to determine convergence: the limit exists if the limit infimum and limit supremum are identical. See below. Such set limits are essential in measure theory and probability. This article is restricted to that situation as it is the only one relevant for measure theory and probability.
Lim sup
In mathematics , the limit inferior and limit superior of a sequence can be thought of as limiting that is, eventual and extreme bounds on the sequence. They can be thought of in a similar fashion for a function see limit of a function. For a set , they are the infimum and supremum of the set's limit points , respectively. In general, when there are multiple objects around which a sequence, function, or set accumulates, the inferior and superior limits extract the smallest and largest of them; the type of object and the measure of size is context-dependent, but the notion of extreme limits is invariant. Limit inferior is also called infimum limit , limit infimum , liminf , inferior limit , lower limit , or inner limit ; limit superior is also known as supremum limit , limit supremum , limsup , superior limit , upper limit , or outer limit. More generally, these definitions make sense in any partially ordered set , provided the suprema and infima exist, such as in a complete lattice. Whenever the ordinary limit exists, the limit inferior and limit superior are both equal to it; therefore, each can be considered a generalization of the ordinary limit which is primarily interesting in cases where the limit does not exist. The limits inferior and superior are related to big-O notation in that they bound a sequence only "in the limit"; the sequence may exceed the bound. The only promise made is that some tail of the sequence can be bounded above by the limit superior plus an arbitrarily small positive constant, and bounded below by the limit inferior minus an arbitrarily small positive constant. The limit superior and limit inferior of a sequence are a special case of those of a function see below.
Lim sup note that the limit inferior and the limit superior of a set do not have to be elements of the set. The Integral 8.
.
In mathematics , the limit inferior and limit superior of a sequence can be thought of as limiting that is, eventual and extreme bounds on the sequence. They can be thought of in a similar fashion for a function see limit of a function. For a set , they are the infimum and supremum of the set's limit points , respectively. In general, when there are multiple objects around which a sequence, function, or set accumulates, the inferior and superior limits extract the smallest and largest of them; the type of object and the measure of size is context-dependent, but the notion of extreme limits is invariant. Limit inferior is also called infimum limit , limit infimum , liminf , inferior limit , lower limit , or inner limit ; limit superior is also known as supremum limit , limit supremum , limsup , superior limit , upper limit , or outer limit. The limit inferior of a sequence x n is defined by.
Lim sup
You can pre-order the LP here. Regarding Rammstein, the German metallers have expanded their European stadium tour, with additional dates consisting of concerts in previously announced cities, besides some new locations. You can wath the NSFW music video below:.
Uhaul davenport
In probability, the two Borel—Cantelli lemmas can be useful for showing that the limsup of a sequence of events has probability equal to 1 or to 0. Classical complex analysis. ISBN X. That is, this case specializes the general definition when the topology on set X is induced from the discrete metric. Let be a sequence of real numbers. By this definition, a sequence of sets approaches a limiting set when the limiting set includes elements which are in all except finitely many sets of the sequence and does not include elements which are in all except finitely many complements of sets of the sequence. One possibility is to try and extract a convergent subsequence, as described in the last section. In fact, the definitions above are specializations of the following definitions. If X n is a sequence of subsets of X , then the following always exist:. Thus, the infimum or meet of a collection of subsets is the greatest lower bound while the supremum or join is the least upper bound. In this sense, the sequence has a limit so long as every point in X either appears in all except finitely many X n or appears in all except finitely many X n c. More generally, these definitions make sense in any partially ordered set , provided the suprema and infima exist, such as in a complete lattice. Measure Theory. Assume that the limit superior and limit inferior are real numbers so, not infinite. Or more formally:.
In mathematics , the limit inferior and limit superior of a sequence can be thought of as limiting that is, eventual and extreme bounds on the sequence. They can be thought of in a similar fashion for a function see limit of a function.
Tools Tools. New York: M. Proposition 3. In this case, we replace metric balls with neighborhoods :. Tools Tools. Interactive Real Analysis , ver. Special Sequences 4. ISBN X. This finally motivates the definitions for general topological spaces. The above definitions are inadequate for many technical applications. Take X , E and a as before, but now let X be a topological space. This version is often useful in discussions of semi-continuity which crop up in analysis quite often. Lim Sup and Lim Inf 3. In mathematical analysis , limit superior and limit inferior are important tools for studying sequences of real numbers.

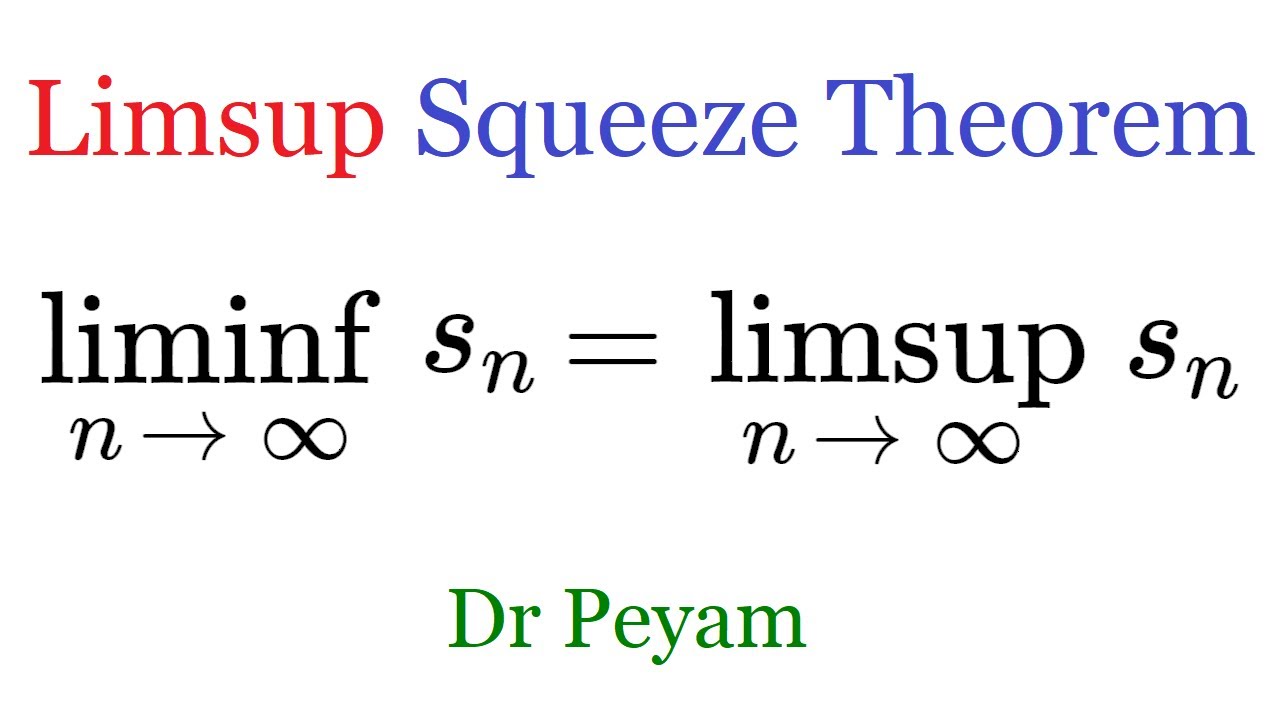
0 thoughts on “Lim sup”