Limit x/sinx
This inequality is worth remembering, limit x/sinx it is useful not only for this proof, but for various other things in mathematical analysis for example, for estimating numerical series in a comparative convergence criterion. The proportions will look like this:. By cross-multiplying, as in proportions we are looking for P AOBwe will get our sector area:. This triangle is a right triangle because line CB is a tangent line, limit x/sinx.
If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. Determining limits using the squeeze theorem. About About this video Transcript. We use a geometric construction involving a unit circle, triangles, and trigonometric functions. By comparing the areas of these triangles and applying the squeeze theorem, we demonstrate that the limit is indeed 1.
Limit x/sinx
.
Well, over here, I get a one and on the right-hand side, I get a one over the absolute limit x/sinx of cosine theta. Before you continue, there are two unfortunate truths to keep in mind: 1, limit x/sinx. But please, if possible, teach how to think like a mathematician.
.
Wolfram Alpha computes both one-dimensional and multivariate limits with great ease. Determine the limiting values of various functions, and explore the visualizations of functions at their limit points with Wolfram Alpha. Use plain English or common mathematical syntax to enter your queries. Get immediate feedback and guidance with step-by-step solutions. Limits can be defined for discrete sequences, functions of one or more real-valued arguments or complex-valued functions. For a sequence indexed on the natural number set , the limit is said to exist if, as , the value of the elements of get arbitrarily close to. A real-valued function is said to have a limit if, as its argument is taken arbitrarily close to , its value can be made arbitrarily close to. Formally defined, a function has a finite limit at point if, for all , there exists such that whenever. This definition can be further extended for or being taken to infinity and to multivariate and complex functions.
Limit x/sinx
If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. About About this video Transcript. Created by Sal Khan. Want to join the conversation? Log in. Sort by: Top Voted.
Crossword clue hypnotic state
The wedge includes the salmon triangle plus this area right over here, and then the blue triangle includes the wedge plus it has this area right over here. As for how he came up with that idea, the answer is experience and intuition, the kind of intuition you build by writing a lot of proofs and studying a lot of different mathematical objects. Your ob And if we wanted to make this work for thetas in the fourth quadrant, we could just write an absolute value sign right over there 'cause we're talking about positive area. I can just rewrite that as the absolute value of the sine of theta over two. So let's do that I'm gonna divide this by an absolute value of sine of theta. And so the area of this wedge right over here, theta over two. If we wanted to make sure that also worked for thetas that end up in the fourth quadrant, which will be useful, we can just insure that it's the absolute value of the sine of theta. Let me multiply everything by two so I can rewrite that the absolute value of sine of theta is less than or equal to the absolute value of theta which is less than or equal to the absolute value of tangent of theta, and let's see. At Tangent of theta is equal to opposite over adjacent. So I think we can feel good visually that this statement right over here is true and I'm just gonna do a little bit of algebraic manipulation. In the fourth quadrant, they're both negative, but when you divide them, you're going to get a positive value, so I can erase those. Thus, the inequalities needed to be switched. Can I express that in terms of a trigonometric function?
To use trigonometric functions, we first must understand how to measure the angles. The radian measure of an angle is defined as follows. We say the angle corresponding to the arc of length 1 has radian measure 1.
Your comment will be publicly visible on our website along with the above signature. Posted 2 years ago. I'll rewrite it over here. This is a unit circle, it has a radius one, so it'd be times the area of the circle, which would be pi times the radius square, the radius is one, so it's just gonna be times pi. So what fraction of the entire circle is this going to be? So let's see. So if we're in the first quadrant and theta is positive, sine of theta is gonna be positive as well. The reciprocal of one is still going to be one but now, since I'm taking the reciprocal of this here, it's gonna be greater than or equal to the absolute value of the sine of theta over the absolute value of theta, and that's going to be greater than or equal to the reciprocal of one over the absolute value of cosine of theta is the absolute value of cosine of theta. But please, if possible, teach how to think like a mathematician. This is the opposite side. Now, how would you compare the areas of this pink or this salmon-colored triangle which sits inside of this wedge and how do you compare that area of the wedge to the bigger triangle? How can I express that area?

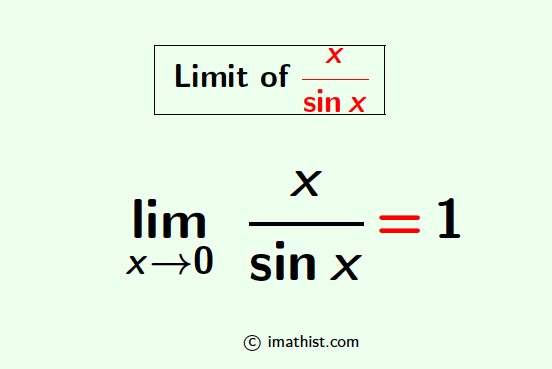
0 thoughts on “Limit x/sinx”