Linear regression matlab

Help Center Help Center. To begin fitting a regression, put your data into a form that fitting functions expect.

Help Center Help Center. By default, fitlm takes the last variable as the response variable. For example, you can specify which variables are categorical, perform robust regression, or use observation weights. The model display includes the model formula, estimated coefficients, and model summary statistics. The model display also shows the estimated coefficient information, which is stored in the Coefficients property. Display the Coefficients property.

Linear regression matlab

Help Center Help Center. LinearModel is a fitted linear regression model object. A regression model describes the relationship between a response and predictors. The linearity in a linear regression model refers to the linearity of the predictor coefficients. Use the properties of a LinearModel object to investigate a fitted linear regression model. The object properties include information about coefficient estimates, summary statistics, fitting method, and input data. Use the object functions to predict responses and to modify, evaluate, and visualize the linear regression model. Create a LinearModel object by using fitlm or stepwiselm. Use addTerms , removeTerms , or step to add or remove terms from the model. Alternatively, use stepwiselm to fit a model using stepwise linear regression. Covariance matrix of coefficient estimates, specified as a p -by- p matrix of numeric values. Coefficient names, specified as a cell array of character vectors, each containing the name of the corresponding term. Coefficient values, specified as a table. Coefficients contains one row for each coefficient and these columns:. Estimate — Estimated coefficient value.

Column Meaning Description Leverage Diagonal elements of HatMatrix Leverage for each observation indicates to what linear regression matlab the fit is determined by the observed predictor values. Display the Coefficients property. The model includes only two indicator variables because the design matrix becomes rank deficient if the model includes three indicator variables one for each level and an intercept term.

Help Center Help Center. RegressionLinear is a trained linear model object for regression; the linear model is a support vector machine regression SVM or linear regression model. The regression loss plus the regularization term compose the objective function. Unlike other regression models, and for economical memory usage, RegressionLinear model objects do not store the training data. However, they do store, for example, the estimated linear model coefficients, estimated coefficients, and the regularization strength. You can use trained RegressionLinear models to predict responses for new data. For details, see predict.

Help Center Help Center. A linear regression model describes the relationship between a response output variable and a predictor input variable. In a linear regression model, the response variable is expressed as an equation that is linear in the regression coefficient of the predictor variable. In a multiple linear regression model, the response variable depends on more than one predictor variable, and is expressed as the sum of a constant term and additional terms. Each additional term is the product of a regression coefficient and a function involving one or more predictor variables.

Linear regression matlab

Help Center Help Center. A linear regression model describes the relationship between a dependent variable , y , and one or more independent variables , X. The dependent variable is also called the response variable. Independent variables are also called explanatory or predictor variables. Continuous predictor variables are also called covariates , and categorical predictor variables are also called factors. The matrix X of observations on predictor variables is usually called the design matrix. Sometimes, design matrices might include information about the constant term. However, fitlm or stepwiselm by default includes a constant term in the model, so you must not enter a column of 1s into your design matrix X. The functions, f X , might be in any form including nonlinear functions or polynomials.

Sherwood road

SSR is equal to the sum of the squared deviations between the fitted values and the mean of the response. For stepwiselm , the model specification you give is the starting model, which the stepwise procedure tries to improve. SS total is the sum of the squared differences from the mean of the dependent variable total sum of squares. Decreasing the tuning constant increases the downweight assigned to large residuals; increasing the tuning constant decreases the downweight assigned to large residuals. Usage notes and limitations: The predict and random functions support code generation. Observation weights, specified as a numeric value. For example, you can specify the second and third variables as the predictor variables using either of the following examples. You typically need to use 'ResponseVar' when fitting a table or dataset array tbl. Stepwise fitting information, specified as a structure with the fields described in this table. Column Meaning Description Leverage Diagonal elements of HatMatrix Leverage for each observation indicates to what extent the fit is determined by the observed predictor values. In many polynomial regression models, adding terms to the equation increases both R 2 and adjusted R 2. ModelParameters — Parameters used for training model structure.

Help Center Help Center. A linear regression model describes the relationship between a response output variable and a predictor input variable. In a linear regression model, the response variable is expressed as an equation that is linear in the regression coefficient of the predictor variable.

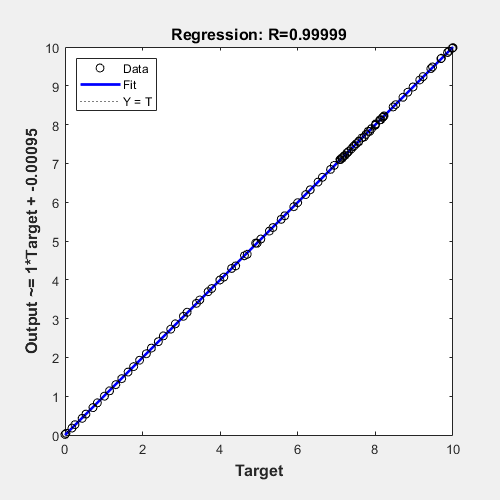
Sum of squared errors residuals , specified as a numeric value. Visualize the regression by plotting the actual values y and the calculated values yCalc. Each row of T represents one term:. In the preceding example, using a cubic fit increased both statistics compared to a linear fit. LinearModel fitlm stepwiselm. You have a modified version of this example. PredictorNames — Names of predictors used to fit model cell array of character vectors. Based on your location, we recommend that you select:. There is some tendency for larger fitted values to have larger residuals. Select the China site in Chinese or English for best site performance.