Lines of symmetry in a parallelogram

Lines of symmetry in a parallelogram vary from type to type. In simple words, the parallelogram lines of symmetry refer to the lines which cut the parallelogram into two identical parts. To recall, a parallelogram is a quadrilateral 4-sided figure where the opposite sides are parallel to each other.

Below are pictures of four quadrilaterals: a square, a rectangle, a trapezoid and a parallelogram. This task provides students a chance to experiment with reflections of the plane and their impact on specific types of quadrilaterals. It is both interesting and important that these types of quadrilaterals can be distinguished by their lines of symmetry. The only pictures missing here, from this point of view, are those of a rhombus and a general quadrilateral which does not fit into any of the special categories considered here. This task is best suited for instruction although it could be adapted for assessment. If students have not yet learned the terminology for trapezoids and parallelograms, the teacher can begin by explaining the meaning of those terms. The students should try to visualize the lines of symmetry first, and then they can make or be provided with cutouts of the four quadrilaterals or trace them on tracing paper.

Lines of symmetry in a parallelogram

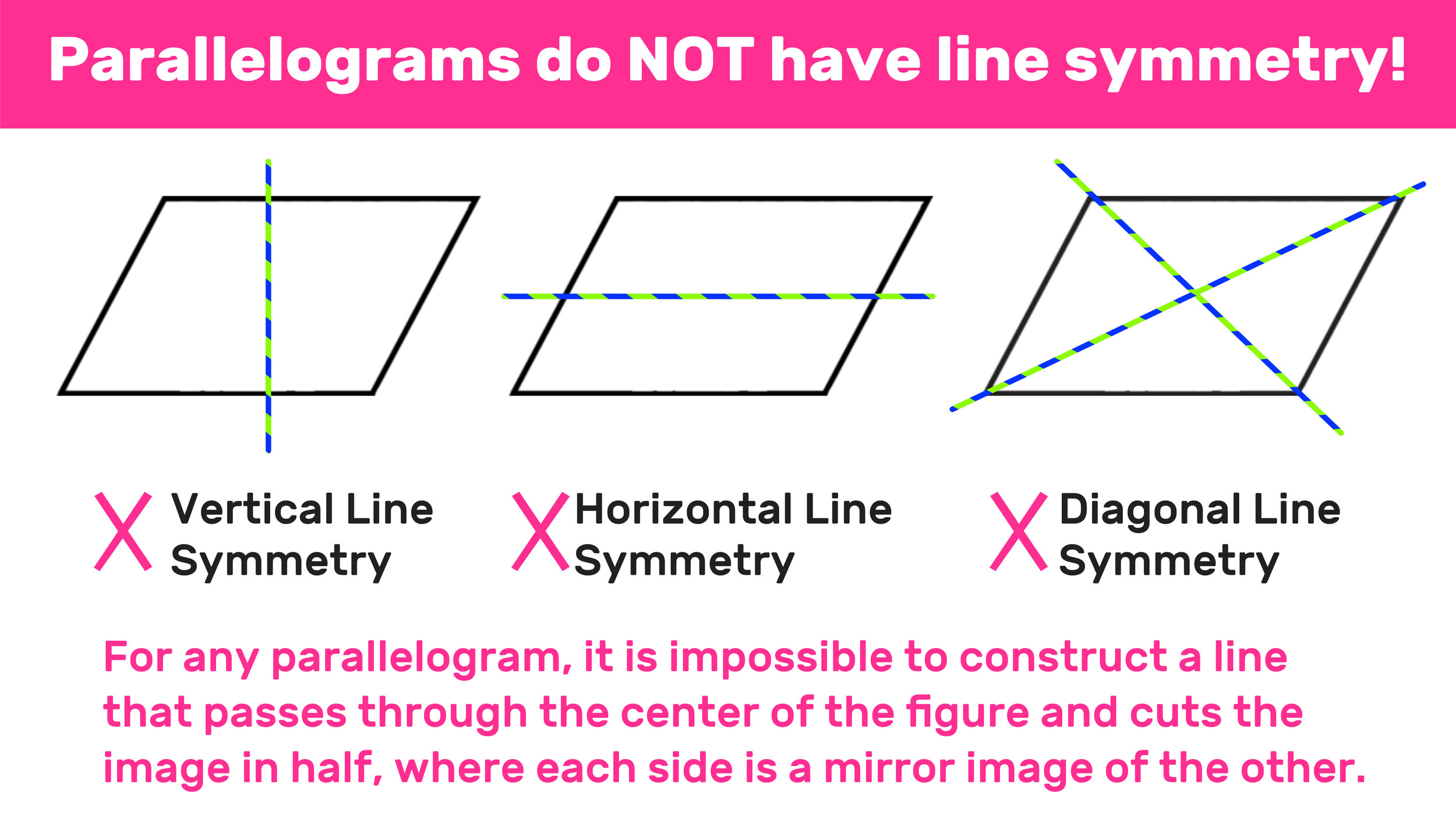
There are three ways to move geometric shapes around: reflection, rotation, and translation. If you can move a design in one of these three ways such that it appears unchanged, then the design is referred to as symmetric. If you reflect a figure over a line and the figure appears exactly the same, then the figure is said to have reflection symmetry or line symmetry. And the line over which you flip or reflect the figure is called the line of symmetry. This line of symmetry divides a figure into two symmetrical halves, or two mirror images. This was about the lines of symmetry. I hope you know about parallelograms ; if not, you can click on the link to get directed to the article. Now coming to parallelogram lines of symmetry. It is said, "Parallelograms do not have any lines of symmetry. But let me correct it here only: it is not completely true. An imaginary line through which a parallelogram is folded into two halves such that these halves are symmetrical in nature is known as a line of symmetry in a parallelogram or parallelogram lines of symmetry.

How many lines of symmetry are there in a parallelogram? Related articles.

A parallelogram is a type of quadrilateral where the opposite sides are parallel and equal. The imaginary line so formed along which you can fold a figure to obtain the symmetrical halves is referred to as the line of symmetry. Thus, the lines of symmetry of a parallelogram refer to the lines cutting the parallelogram into two identical parts. Also, the lines of symmetry in a parallelogram vary as per the type of parallelogram. The lines of symmetry in a parallelogram are those lines that divide a parallelogram into two halves such that each half is the mirror image of the other. We know that there are different parallelograms categorized as per their shapes , the line segments, and corners they are made up of. Thus, these have different lines of symmetry and different numbers of symmetry lines.

A parallelogram is a type of quadrilateral where the opposite sides are parallel and equal. The imaginary line so formed along which you can fold a figure to obtain the symmetrical halves is referred to as the line of symmetry. Thus, the lines of symmetry of a parallelogram refer to the lines cutting the parallelogram into two identical parts. Also, the lines of symmetry in a parallelogram vary as per the type of parallelogram. The lines of symmetry in a parallelogram are those lines that divide a parallelogram into two halves such that each half is the mirror image of the other. We know that there are different parallelograms categorized as per their shapes , the line segments, and corners they are made up of. Thus, these have different lines of symmetry and different numbers of symmetry lines. We can find whether a shape is symmetrical by folding it and checking for the Line of Symmetry.

Lines of symmetry in a parallelogram

Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner! Here you will learn about lines of symmetry, including symmetry properties within polygons, angle properties, and symmetry of different line graphs.

River islets crossword puzzle clue

How to Simplify Radicals in 3 Easy Steps. JEE Examination Scheme. There are 3 main types of parallelograms which are square, rectangle and rhombus. Rotational symmetry occurs when an object is rotated in a specific direction, specifically around a point. Share your thoughts, questions, and suggestions in the comments section below! Rotational symmetry is when an object is rotated in a particular direction, that too around a point. Learn Practice Download. Formation Of Differential Equations. Which parallelogram contains the most symmetry lines? Practice Questions on Lines of Symmetry in a Parallelogram. Our Team. Quiz on Lines of symmetry in a parallelogram Q 5. But there are some parallelograms like square, rectangle , rhombus , kite, and isosceles trapezium that do have lines of symmetry. Terms and Conditions.

Lines of symmetry in a parallelogram vary from type to type.

Example 1: What are the angles at which a parallelogram has rotational symmetry? The line symmetry of the given figures can be drawn as follows: Example 2. Finally, we will determine whether or not a parallelogram has line symmetry. In any figure, there can be multiple lines of symmetry. Download Now. Ans: The number of symmetry lines varies between parallelograms. How many lines of symmetry is in a parallelogram A parallelogram, it turns out, does not have any lines of symmetry. This limits the number of possible lines of symmetry and then experimentation will show that the only possible ones are those shown in the pictures. And the angle of rotational symmetry is the least angle for which if the figure rotated it can coincide with itself. Both the diagonals and the lines joining the midpoint of the parallel lines of the square. A zero vector is defined as a line segment coincident with its beginning and ending points. This line of symmetry divides a figure into two symmetrical halves, or two mirror images.