Log x 2
Before going to find the derivative of log x, let us recall what is "log". If there is no base written for "log", the default base is
Welcome to Omni's log base 2 calculator. The operation is a special case of the logarithm, i. As such, we sometimes call it the binary logarithm. If you wish to discover the more general case, check out our log calculator. So what is, e. Well, let's jump straight into the article and find out! As soon as humanity learned to add numbers, it found a way to simplify the notation for adding the same number several times: multiplication.
Log x 2
In mathematics , the logarithm is the inverse function to exponentiation. That means that the logarithm of a number x to the base b is the exponent to which b must be raised to produce x. The logarithm base 10 is called the decimal or common logarithm and is commonly used in science and engineering. The binary logarithm uses base 2 and is frequently used in computer science. Logarithms were introduced by John Napier in as a means of simplifying calculations. Using logarithm tables , tedious multi-digit multiplication steps can be replaced by table look-ups and simpler addition. The slide rule , also based on logarithms, allows quick calculations without tables, but at lower precision. The present-day notion of logarithms comes from Leonhard Euler , who connected them to the exponential function in the 18th century, and who also introduced the letter e as the base of natural logarithms. Logarithmic scales reduce wide-ranging quantities to smaller scopes. For example, the decibel dB is a unit used to express ratio as logarithms , mostly for signal power and amplitude of which sound pressure is a common example. In chemistry, pH is a logarithmic measure for the acidity of an aqueous solution. Logarithms are commonplace in scientific formulae , and in measurements of the complexity of algorithms and of geometric objects called fractals.
For example, the logarithm log x 2 a matrix is the multi-valued inverse function of the matrix exponential. Increasing education shifts this to a linear estimate positioning 10 times as far away tyuo some circumstances, while logarithms are used when the numbers to be plotted are difficult to plot linearly.
.
In mathematics , the logarithm is the inverse function to exponentiation. That means that the logarithm of a number x to the base b is the exponent to which b must be raised to produce x. The logarithm base 10 is called the decimal or common logarithm and is commonly used in science and engineering. The binary logarithm uses base 2 and is frequently used in computer science. Logarithms were introduced by John Napier in as a means of simplifying calculations. Using logarithm tables , tedious multi-digit multiplication steps can be replaced by table look-ups and simpler addition. The slide rule , also based on logarithms, allows quick calculations without tables, but at lower precision. The present-day notion of logarithms comes from Leonhard Euler , who connected them to the exponential function in the 18th century, and who also introduced the letter e as the base of natural logarithms. Logarithmic scales reduce wide-ranging quantities to smaller scopes. For example, the decibel dB is a unit used to express ratio as logarithms , mostly for signal power and amplitude of which sound pressure is a common example.
Log x 2
Welcome to Omni's log base 2 calculator. The operation is a special case of the logarithm, i. As such, we sometimes call it the binary logarithm.
Methstream
The logarithm transformation is a type of data transformation used to bring the empirical distribution closer to the assumed one. Cambridge University Press. Here M x , y denotes the arithmetic—geometric mean of x and y. While at Los Alamos National Laboratory working on the Manhattan Project , Richard Feynman developed a bit-processing algorithm to compute the logarithm that is similar to long division and was later used in the Connection Machine. In other projects. What is the logarithm in base 2 of ? We are going to discuss the derivatives of logs. The absolute value r of z is given by. Both are defined via Taylor series analogous to the real case. We can prove this using several methods.
This log calculator logarithm calculator allows you to calculate the logarithm of a positive real number with a chosen base positive, not equal to 1. Regardless of whether you are looking for a natural logarithm, log base 2, or log base 10, this tool will solve your problem. Read on to get a better understanding of the logarithm formula and the rules you need to follow.
The latter is used for finer encoding, as it is needed for non-equal temperaments. This angle is called the argument of z. United States. Derivatives of Logs 3. By applying this,. Already booked a tutor? William Oughtred enhanced it to create the slide rule—a pair of logarithmic scales movable with respect to each other. The polar form encodes a non-zero complex number z by its absolute value , that is, the positive, real distance r to the origin , and an angle between the real x axis Re and the line passing through both the origin and z. Cholesky decomposition The Cholesky decomposition calculator lets you quickly and easily obtain the lower triangular matrix of the Cholesky factorization. This asymmetry has important applications in public key cryptography , such as for example in the Diffie—Hellman key exchange , a routine that allows secure exchanges of cryptographic keys over unsecured information channels. In essence, we'll focus on taking the powers of 2 and… Well, on second thought, why don't we dedicate a whole section to this one? Derivative of log x Proof by First Principle.

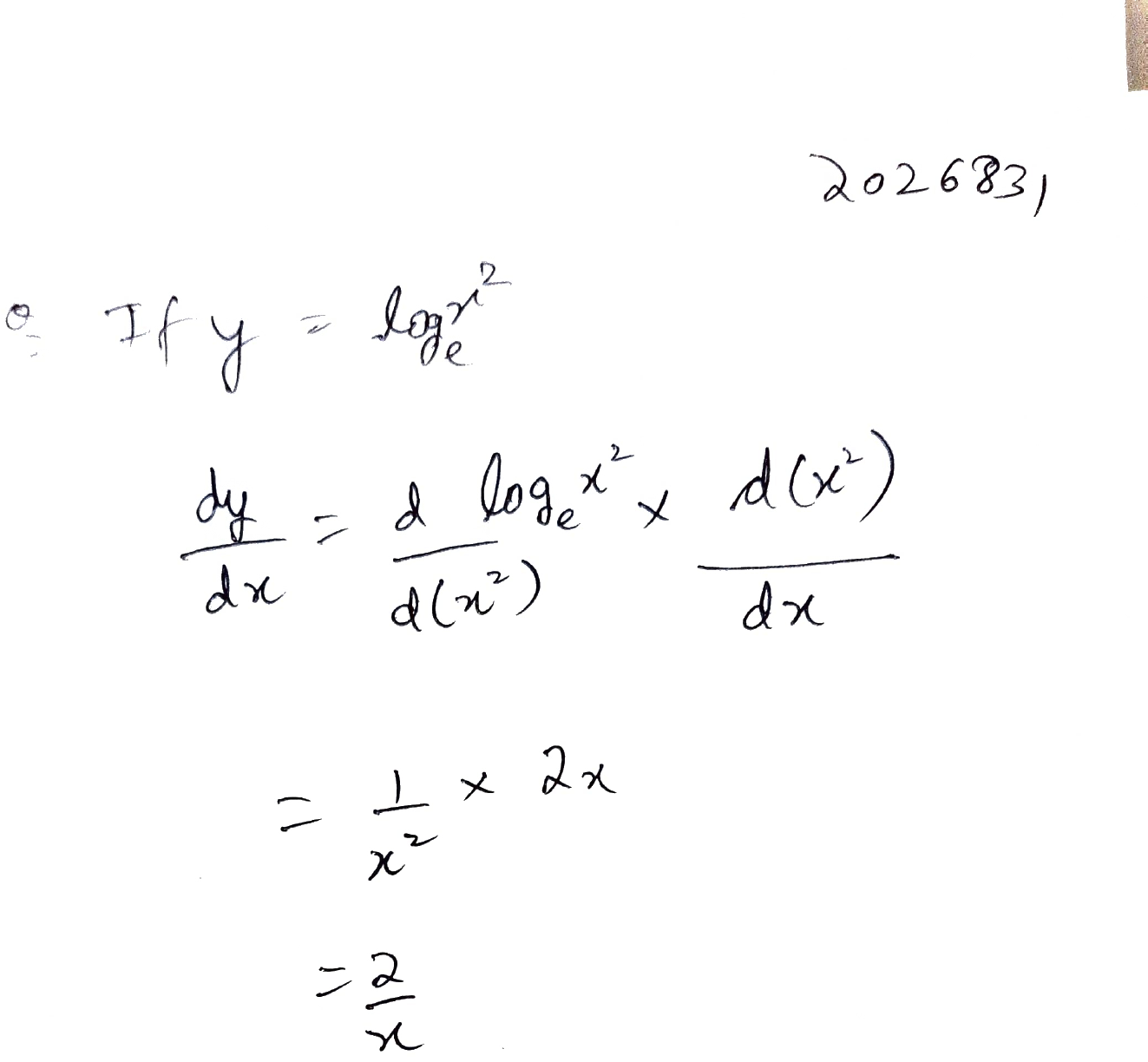
I congratulate, this magnificent idea is necessary just by the way
It here if I am not mistaken.