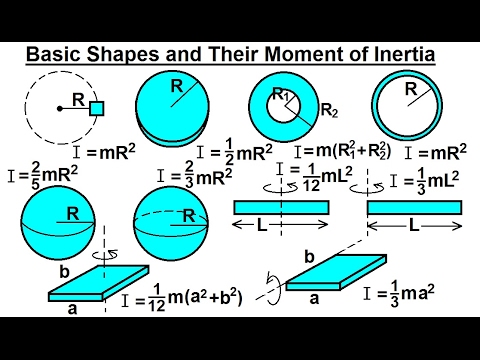
Moment of inertia formula disk

In the preceding subsection, we defined the moment of inertia but did not show how to calculate it. In this subsection, we show how to calculate moment of inertia formula disk moment of inertia for several standard types of objects, as well as how to use known moments of inertia to find the moment one direction imagines inertia for a shifted axis or for a compound object. This section is very useful for seeing how to apply a general equation to complex objects a skill that is critical for more advanced physics and engineering courses.

When we talk about the moment of inertia of a disk we can say that it is quite similar to that for a solid cylinder with any given measure of length. However, for a disk, we have to take it as a special character. Generally, it is used as a base for building the moment of inertia expression for different other shapes, such as a cylinder or a sphere. Meanwhile, we can also find the moment of inertia of a circular disc with respect to different situations. They are as follows;.

Moment of inertia formula disk

The moment of inertia of an annular disk can be found by finding the mass of a small elemental ring inside the disk to integrate the MOI formula of the annular disk. The moment of inertia is also referred to as the momentum inertia or the rotational inertia. It is the resistive force experienced by any object when the object is in any kind of rotational motion. Speaking about the MOI or the moment of inertia of an annular disk. Before going into that we must understand what an annular disk is. An annular disk is similar to a normal disk. However, unlike a normal disk, it has a hollow space inside it. Therefore, it has two radii, an inner radius and an outer radius. To find out the moment of inertia of an annular disk, we will consider a small elemental ring inside the annular disk having a radius of r and width of dr along with the thickness t. That can also be considered as the small elemental volume inside the annular disk. We are initially going to find out the moment of inertia of that ring or the elemental volume and then integrate it having the limitations of the radius of the disk to find out the moment of inertia of the complete annular disk. In this article, we are going to learn how to derive the moment of inertia formula of an annular disk. Before going into the derivation, let us understand the annotations used and the annular disk using a diagram. The axis of rotation in this derivation is considered the Z-axis, which is also the axis of the disk itself. Also consider the small elemental volume inside this annular disk having radius r, thickness t and width dr.

Description Figure Moment s of inertia Point mass M at a distance r from the axis of rotation. The moment of inertia of an annular disk is given by the equation

Moment of inertia , denoted by I , measures the extent to which an object resists rotational acceleration about a particular axis , it is the rotational analogue to mass which determines an object's resistance to linear acceleration. It should not be confused with the second moment of area , which has units of dimension L 4 [length] 4 and is used in beam calculations. The mass moment of inertia is often also known as the rotational inertia , and sometimes as the angular mass. For simple objects with geometric symmetry, one can often determine the moment of inertia in an exact closed-form expression. Typically this occurs when the mass density is constant, but in some cases the density can vary throughout the object as well.

Moment of inertia of an annular disc that is uniform and having mass m , thickness t , inner radius R 1 and outer radius R 2 is expressed as;. We will start by recalling the moment of inertia expression which is given as;. In this, we can consider dm as the mass of volume dV. We will then first consider the moment of inertia about the z-axis and we get the expression;. Like the relation in a disc, the mass dm of the volume element dV is related to volume and density by;. We then have to calculate dV. Here we will assume that the disc will have a uniform density. Here we will also consider a ring to be at radius r with width dr and thickness t. We will get;.

Moment of inertia formula disk

Imagine a merry-go-round spinning around its central axis. Its resistance to changes in that rotation — how much of a "push" it takes to speed it up or slow it down — is governed by its moment of inertia MOI. It quantifies an object's "rotational inertia" around a specific axis. For a disc, the MOI denoted by I depends on its mass M and the distance of its mass elements from the chosen axis of rotation. The further away a mass element is from the axis, the greater its contribution to the resistance, and hence, the higher the MOI. Inertia is a way to understand how movement, time, and energy are connected. When things are in motion, they can also be still, either naturally or by resisting the movement. Resistance occurs when electric charges face opposition in their flow. Now, let's briefly explore the moment of inertia and moment of inertia of a disc to learn more.

Restaurante el rey del bacalao reseñas

A point mass does not have a moment of inertia around its own axis, but using the parallel axis theorem a moment of inertia around a distant axis of rotation is achieved. We again start with the relationship for the surface mass density , which is the mass per unit surface area. After putting all these together we get:. Regular icosahedron of side s and mass m. Right circular cone with radius r , height h and mass m. Share Share Share Call Us. Related articles. A transformer is a device that strips electrons from atoms and uses them to create an electromotive force. UPSC Toppers. Your result is as below. Refer to Table Just as before, we obtain.

If you're seeing this message, it means we're having trouble loading external resources on our website.

View subscription plans. Ellipsoid solid of semiaxes a , b , and c with mass m. Physics for Scientists and Engineers 2nd ed. At a step, we again need to find the mass of the disk to solve the equation, thus finding the same by subtracting the mass of the whole disk with radius R2 from that of R1 and substituting the value and solving it. Factors affecting mass moment of Inertia are:. The concept of parallel and perpendicular axes can be applied to find the MOI about other axes e. The moment of inertia of a thin circular disk is the same as that for a solid cylinder of any length, but it deserves special consideration because it is often used as an element for building up the moment of inertia expression for other geometries, such as the sphere or the cylinder about an end diameter. Beer and E. Consequently, the tire will tend to wobble, and a periodic torque must be exerted by the axle of the car to keep it rolling straight. Thin rectangular plate of height h , width w and mass m Axis of rotation at the end of the plate. Principal Axes The use of Newton's second law for rotation involves the assumption that the axis about which the rotation is taking place is a principal axis. We want a thin rod so that we can assume the cross-sectional area of the rod is small and the rod can be thought of as a string of masses along a one-dimensional straight line. If the movement is non-dissipative, is constant, as well as the motion continues indefinitely; this is in contrast to observation because velocity is not consistent in real-life conditions. Learn more topics related to Physics. This list of moment of inertia tensors is given for principal axes of each object.