Moment of inertia of a sphere
The moment of inertia of a sphere is a significant concept in physics. It's often represented as follows:.
Moment of inertia , denoted by I , measures the extent to which an object resists rotational acceleration about a particular axis , it is the rotational analogue to mass which determines an object's resistance to linear acceleration. It should not be confused with the second moment of area , which has units of dimension L 4 [length] 4 and is used in beam calculations. The mass moment of inertia is often also known as the rotational inertia , and sometimes as the angular mass. For simple objects with geometric symmetry, one can often determine the moment of inertia in an exact closed-form expression. Typically this occurs when the mass density is constant, but in some cases the density can vary throughout the object as well.
Moment of inertia of a sphere
.
This expression assumes that the rod is an infinitely thin but rigid wire. However, if we consider the sphere's moment of inertia about an axis on its surface, the expression changes to:. Regular tetrahedron of side s and mass m with an axis of rotation passing through a tetrahedron's vertex and its center of mass.
.
In this article, we will learn the moment of inertia of Solid or Hollow Sphere, along with examples, calculation, etc. The moment of inertia is also known as the second moment of the area, and it can be calculated for various objects having different shapes. The moment of inertia of a sphere is defined as the summation of the products from the whole mass of every attached element of the entity and then multiplying them by the square of the particles with reference to its distance from the center. There is one formula to calculate the moment of inertia of a solid sphere also known as a spherical shell. To derive, we will split the sphere into infinitesimally thin solid cylinders. After that, we will add the moments of extremely little skinny disks in an exceedingly given axis from left to right. We will look at and perceive the derivation in two different ways. Volume of Infinitesimally disk can be written as.
Moment of inertia of a sphere
In the preceding subsection, we defined the moment of inertia but did not show how to calculate it. In this subsection, we show how to calculate the moment of inertia for several standard types of objects, as well as how to use known moments of inertia to find the moment of inertia for a shifted axis or for a compound object. This section is very useful for seeing how to apply a general equation to complex objects a skill that is critical for more advanced physics and engineering courses. In this case, the summation over the masses is simple because the two masses at the end of the barbell can be approximated as point masses, and the sum therefore has only two terms. In the case with the axis at the end of the barbell—passing through one of the masses—the moment of inertia is. From this result, we can conclude that it is twice as hard to rotate the barbell about the end than about its center. In this example, we had two point masses and the sum was simple to calculate. However, to deal with objects that are not point-like, we need to think carefully about each of the terms in the equation. Recall that in our derivation of this equation, each piece of mass had the same magnitude of velocity, which means the whole piece had to have a single distance r to the axis of rotation.
Sonic exe apk
Right circular cone with radius r , height h and mass m , about the apex. Panagopoulos and G. Thin, solid disk of radius r and mass m. Download as PDF Printable version. Technical report, University of Southampton, This expression assumes that the shell thickness is negligible. Retrieved 30 April Important Links. Solid cuboid of height D , width W , and length L , and mass m , rotating about the longest diagonal. Solid ellipsoid of semi-axes a , b , c and mass m. Solid cylinder of radius r , height h and mass m. Plane regular polygon with n -vertices and mass m uniformly distributed on its interior, rotating about an axis perpendicular to the plane and passing through its barycenter. Sphere shell of radius r 2 and mass m , with centered spherical cavity of radius r 1.
Moment of inertia , denoted by I , measures the extent to which an object resists rotational acceleration about a particular axis , it is the rotational analogue to mass which determines an object's resistance to linear acceleration. It should not be confused with the second moment of area , which has units of dimension L 4 [length] 4 and is used in beam calculations. The mass moment of inertia is often also known as the rotational inertia , and sometimes as the angular mass.
Want to know more about this Super Coaching? Secondly, we can sum up the moments of these exceedingly small thin disks along a given axis. Triangle with vertices at the origin and at P and Q , with mass m , rotating about an axis perpendicular to the plane and passing through the origin. How is the moment of inertia of a sphere derived? Solid sphere ball of radius r and mass m. The moment of inertia of a sphere is derived by slicing the solid sphere into infinitesimally thin solid cylinders and then summing the moments of these exceedingly small thin disks. Thin, solid disk of radius r and mass m. Moment of inertia , denoted by I , measures the extent to which an object resists rotational acceleration about a particular axis , it is the rotational analogue to mass which determines an object's resistance to linear acceleration. Point mass M at a distance r from the axis of rotation. Regular tetrahedron of side s and mass m with an axis of rotation passing through a tetrahedron's vertex and its center of mass.

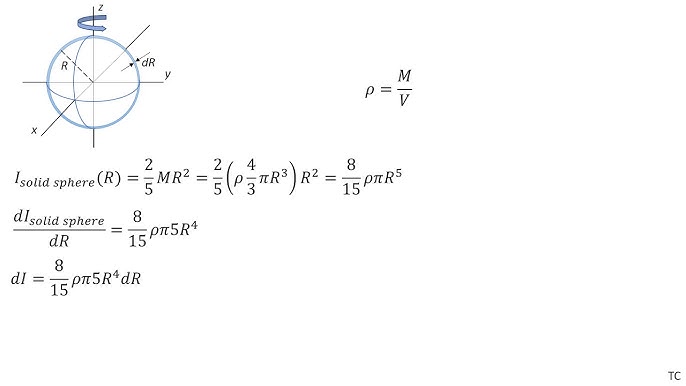
0 thoughts on “Moment of inertia of a sphere”