Normal and tangential components

In mathematicsgiven a vector at a point on a curvethat vector can be decomposed uniquely as a sum of two vectors, one tangent to the curve, called the tangential component of the vector, and another one perpendicular to the normal and tangential components, called the normal component of the vector.

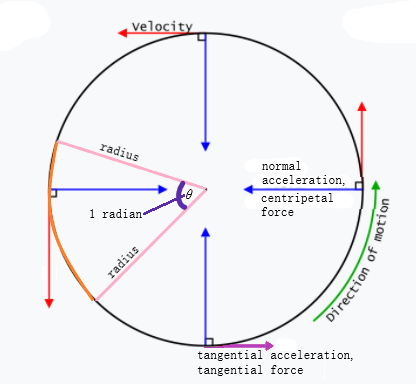
We can obtain the direction of motion from the velocity. If we stay on a straight course, then our acceleration is in the same direction as our motion, and would only cause us to speed up or slow down. We'll call this tangential acceleration. If we want to design a roller coaster, build an F15 fighter plane, send a satellite in orbit, or construct anything that doesn't move in a straight line, we need to understand how acceleration causes us to leave a straight path. We may still be speeding up or slowing down tangential acceleration , but now we'll have a component that veers us off the straight path. We'll call this normal acceleration, it's orthogonal to the velocity.

Normal and tangential components

This section breaks down acceleration into two components called the tangential and normal components. The addition of these two components will give us the overall acceleration. We're use to thinking about acceleration as the second derivative of position, and while that is one way to look at the overall acceleration, we can further break down acceleration into two components: tangential and normal acceleration. Remember that vectors have magnitude AND direction. The tangential acceleration is a measure of the rate of change in the magnitude of the velocity vector, i. This approach to acceleration is particularly useful in physics applications, because we need to know how much of the total acceleration acts in any given direction. Think for example of designing brakes for a car or the engine of a rocket. Why might it be useful to separate acceleration into components? We can find the tangential accelration by using Chain Rule to rewrite the velocity vector as follows:. To calculate the normal component of the accleration, use the following formula:. We can relate this back to a common physics principal-uniform circular motion. In uniform circulation motion, when the speed is not changing, there is no tangential acceleration, only normal accleration pointing towards the center of circle. Why do you think this is?

It is important to be consistent with units.

We have now seen how to describe curves in the plane and in space, and how to determine their properties, such as arc length and curvature. All of this leads to the main goal of this chapter, which is the description of motion along plane curves and space curves. We now have all the tools we need; in this section, we put these ideas together and look at how to use them. Our starting point is using vector-valued functions to represent the position of an object as a function of time. All of the following material can be applied either to curves in the plane or to space curves. For example, when we look at the orbit of the planets, the curves defining these orbits all lie in a plane because they are elliptical. However, a particle traveling along a helix moves on a curve in three dimensions.

We have now seen how to describe curves in the plane and in space, and how to determine their properties, such as arc length and curvature. All of this leads to the main goal of this chapter, which is the description of motion along plane curves and space curves. We now have all the tools we need; in this section, we put these ideas together and look at how to use them. Our starting point is using vector-valued functions to represent the position of an object as a function of time. All of the following material can be applied either to curves in the plane or to space curves.

Normal and tangential components

From Calculus I we know that given the position function of an object that the velocity of the object is the first derivative of the position function and the acceleration of the object is the second derivative of the position function. The tangential component is the part of the acceleration that is tangential to the curve and the normal component is the part of the acceleration that is normal or orthogonal to the curve. If we do this we can write the acceleration as,.

Chopstick styler wand

Find the velocity, acceleration, and speed as functions of time. In wet conditions, the coefficient of friction can become as low as 0. We'll define the torsion vector to be. If this is the case, how fast can the car travel through the bottom of the turn without skidding? If you still need to work on mastering some of the ideas, please do so and then demonstrate your mastery though the quiz corrections. Watch a YouTube Video. To determine this distance, we assume the projectile is fired from ground level and we wish it to return to ground level. The addition of these two components will give us the overall acceleration. The coefficient of friction for a normal tire in dry conditions is approximately 0. Each end of the track is approximately semicircular, so when cars make turns they are traveling along an approximately circular curve. That will be your decision to make. Think ahead years.

This section breaks down acceleration into two components called the tangential and normal components. The addition of these two components will give us the overall acceleration. We're use to thinking about acceleration as the second derivative of position, and while that is one way to look at the overall acceleration, we can further break down acceleration into two components: tangential and normal acceleration.

Before each Celebration of Knowledge we will devote a class period to review. How long will it take for the cannonball to splash into the sea? If you still need to work on mastering some of the ideas, please do so and then demonstrate your mastery though the quiz corrections. You'd see this formula in dynamics , and it shows up on the Fundamentals of Engineering exam where you just have to use the formula, not prove where it comes from. Since planets have closed orbits, the only possibility is an ellipse. To understand centripetal acceleration, suppose you are traveling in a car on a circular track at a constant speed. Therefore, if we know the average distance from a planet to the Sun in astronomical units , we can then calculate the length of its year in Earth years , and vice versa. However, a particle traveling along a helix moves on a curve in three dimensions. Conclude that the maximum speed does not actually depend on the mass of the car. As they pass close enough to the Sun, the gravitational field of the Sun deflects the trajectory enough so the path becomes hyperbolic. Illustration of tangential and normal components of a vector to a surface. This is calculated using reflectors left on the Moon by Apollo astronauts back in the s.