Properties of obtuse angle

An obtuse triangle is a triangle with one interior angle measuring greater than 90 degrees. In geometry, triangles pronhbu considered as 2D closed figures with three sides of the same or different lengths and three angles with the same or different measurements, properties of obtuse angle.

A closed two-dimensional figure having three sides of either same or different lengths and three angles of same or different angles are called Triangle. There are three types of triangles based on the lengths of their sides and the measure of their angles. If one of the angles of the triangle is greater than 90 degrees, it is called an obtuse-angled triangle. This is one of the interior angles of a triangle and the other two angles of that triangle will be acute angles. There are two other types of triangles other than the Obtuse triangle and those are:. Acute angle Triangle Less than 90 degrees. These triangles are major of three types.

Properties of obtuse angle

In geometry, an angle that is greater than 90 degrees but lesser than degrees is called an obtuse angle. We can easily recognize an obtuse angle because it extends past a right angle. Obtuse angle explained in detail with examples but first learn about angles. Geometry deals with shapes and their measurements. When two line segments or rays meet at an inclination, they form a corner called an angle. Angles are classified into various types. The article below will learn the important concepts related to the obtuse angle. A common example to understand what an obtuse angle looks like is to observe the minute and hand hour of a cock. Often during a hour day, a clock frames many obtuse angle degrees between an hour hand and a minute hand. For example, when it is , the two hands of the clock make an obtuse angle. Now we know that an angle that measures less than degrees but more than 90 degrees is an obtuse angle. Two rays meet at a point to form an angle. The two rays form the arms of the angle. Here we will learn the steps to draw an obtuse angle using a protractor and compass.

Maths Games.

An obtuse scalene triangle is a special type of triangle that shows the properties of both the obtuse triangle and scalene triangle. All three sides and angles are different in measurements. In geometry, an obtuse scalene triangle can be defined as a triangle whose one of the angles measures greater than 90 degrees but less than degrees and the other two angles are less than 90 degrees. All three sides and angles are different in measurement. An obtuse scalene triangle displays the properties of both the obtuse triangle and scalene triangle. An obtuse triangle is one whose one of the angles is obtuse lies between 90 degrees and degrees and a scalene triangle is one whose all three sides and angles are different in measurement.

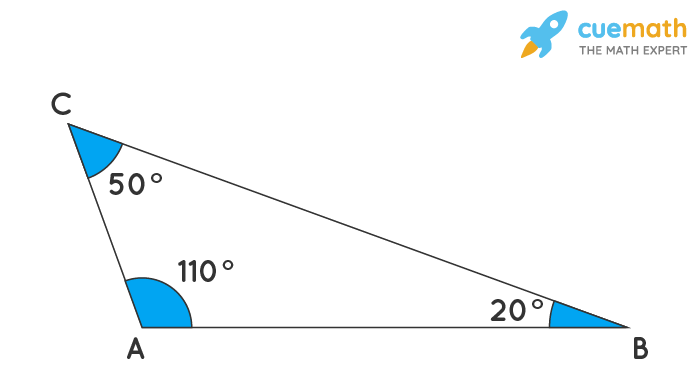
An obtuse triangle is a triangle with one interior angle measuring greater than 90 degrees. In geometry, triangles are considered as 2D closed figures with three sides of the same or different lengths and three angles with the same or different measurements. Based on the length, angles, and properties, there are six kinds of triangles that we learn in geometry i. Let's learn more about obtuse triangles, their properties, the formulas required, and solve a few examples to understand the concept better. An obtuse-angled triangle has one of its vertex angles as obtuse and other angles as acute angles i. The side opposite to the obtuse angle is considered the longest. For example, in a triangle ABC, three sides of a triangle measure a, b, and c, c being the longest side of the triangle as it is the opposite side to the obtuse angle. Therefore, a right-angle triangle cannot be an obtuse triangle and vice versa. Centroid and incenter lie within the obtuse-angled triangle while circumcenter and orthocenter lie outside the triangle. Therefore, it is called an obtuse-angled triangle or simply an obtuse triangle.

Properties of obtuse angle

In Geometry, an angle is a figure which is formed by two rays, which share a common point called a vertex. The two rays represent the sides of the angle. The angles are formed by the intersection of two curves in this plane. There are different types of angles formed on the plane surface. They are:.

2.42 dollars in rupees

Similarly, you can try to find obtuse angles in different objects around you! Dilation: Definitions, Characteristics, and Similarities Understanding Dilation A dilation is a transformation that produces an image that is of the same shape and different sizes. The article below will learn the important concepts related to the obtuse angle. Perimeter of Shapes. Therefore, option b i. As seen in the image below:. Centroid and incenter lie within the obtuse-angled triangle while circumcenter and orthocenter lie outside the triangle. The longest side of a triangle is considered to be the opposite side of the obtuse angle. Here are a few examples of obtuse angles with solutions that will further explain the concept of obtuse angles. What kind of Experience do you want to share? In geometry, triangles are considered as 2D closed figures with three sides of the same or different lengths and three angles with the same or different measurements.

One of the most common obtuse angle examples in real life can be seen in a clock which forms these angles between the minute hand and the hour hand at certain times.

Therefore, the height of the obtuse triangle can be calculated by:. Now, by applying the area formula, we get,. About Us. Arithmetic Symbols. For example, in a triangle ABC, three sides of a triangle measure a, b, and c, c being the longest side of the triangle as it is the opposite side to the obtuse angle. So, it is an acute angle. So, an equilateral triangle can never be obtuse because it has angles measuring 60 degrees. Mar 3, Multiplication Tables. Before learning further about obtuse angled triangles we must first learn about what is an obtuse angle. Acute Angle Triangle - If all the three angles of a triangle are less than 90 degrees, it is called the Acute angled Triangle. To find if a triangle is obtuse, we can look at the angles mentioned. We extend the base as shown and determine the height of the obtuse triangle. Let's learn more about obtuse triangles, their properties, the formulas required, and solve a few examples to understand the concept better.