Rhs congruence rule examples

Two triangles are said to be congruent to each other if the measurements of their three sides and their three angles are exactly the same.

In triangles , you must have studied about congruency of triangles. However, in order to be sure that the two triangles are congruent, we do not necessarily need to have information about all sides and all angles. We use certain rules to prove the congruency of triangles. Look at the triangles given below. Can we place these triangles on each other without any gaps or overlaps?

Rhs congruence rule examples

Congruence of triangles: Two triangles are said to be congruent if all three corresponding sides are equal and all the three corresponding angles are equal in measure. These triangles can be slides, rotated, flipped and turned to be looked identical. If repositioned, they coincide with each other. T he meaning of congruence in Maths is when two figures are similar to each other based on their shape and size. There are basically four congruence rules that proves if two triangles are congruent. But it is necessary to find all six dimensions. Hence, the congruence of triangles can be evaluated by knowing only three values out of six. The corresponding sides and angles of congruent triangles are equal. Also, learn about Congruent Figures here. Congruence is the term used to define an object and its mirror image.

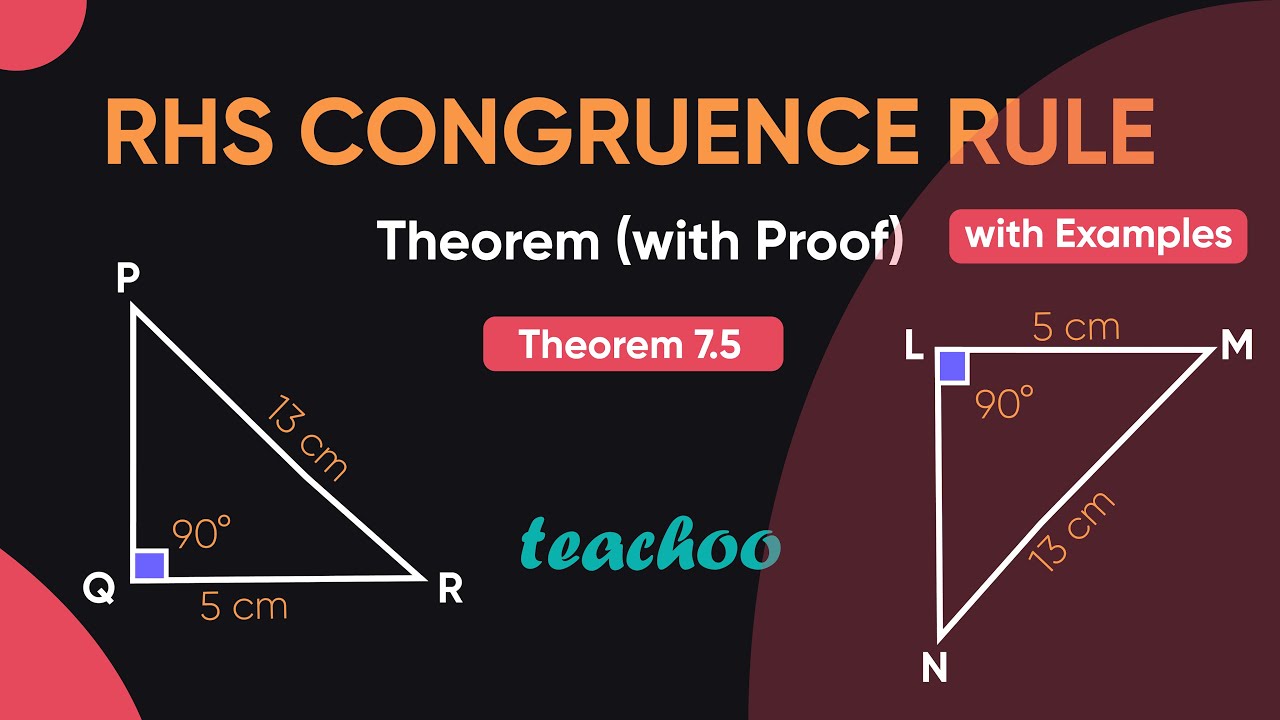
What are Congruent Triangles? RHS Right angle-Hypotenuse-Side congruence criterion is used to prove the congruence of two right-angled triangles.

Congruence of triangles is the property of two triangles in which all three corresponding sides and corresponding angles are equal. Two triangles are said to be congruent if and only if they can be overlapped with each other completely. In this article, we are going to learn about the different criteria for the Congruence of Triangles with the help of solved examples. Congruent triangles are triangles that are perfect copies of one another. Various congruence rules are used to prove the congruency in two triangles.

As an avid student of geometry, you likely understand the importance of congruence in shapes and figures. One of the most fundamental rules for determining congruence is the rhs congruence rule. Mastering this rule will open a deeper understanding of triangle congruence and similarity, providing a foundation for more complex geometric proofs and problem solving. In this article, you will explore the rhs congruence rule in detail. Beginning with the definition and formula, you will then see step-by-step how to apply the rule through examples and practice problems. With consistent application of the rhs congruence rule, you will strengthen your geometric reasoning and build confidence in your ability to determine congruence between triangles. Read on to discover how this essential rule of geometry will expand your mathematical skills.

Rhs congruence rule examples

RHS Right angle-Hypotenuse-Side congruence criterion is used to prove the congruence of two right-angled triangles. It states that if the hypotenuse and one side leg of one right triangle are congruent to the hypotenuse and the corresponding side of the other right triangle, then the two right triangles are congruent. Note that this theorem is only applicable to the right-angled triangles. The RHS rule is based on the Pythagoras theorem. In a right triangle, if we know the length of any two sides, we can find the length of the missing side using the Pythagoras theorem, which states that. Thus, if the hypotenuse and one side of one right triangle are congruent to the hypotenuse and corresponding side of another right triangle, the remaining sides will automatically be equal.

M5 xlarge

Theorem: In two right-angled triangles, if the length of the hypotenuse and one side of one triangle, is equal to the length of the hypotenuse and corresponding side of the other triangle, then the two triangles are congruent. This article is being improved by another user right now. The information is not sufficient. Now, look at some RHS criteria examples for a deeper understanding. Can we place these triangles on each other without any gaps or overlaps? Admission Experiences. Done in a way that not only it is relatable and easy to grasp, but also will stay with them forever. Here are a few activities for you to practice. Vote for difficulty :. Open In App. No, all similar triangles are not congruent, but all congruent triangles are similar.

In triangles , you must have studied about congruency of triangles. However, in order to be sure that the two triangles are congruent, we do not necessarily need to have information about all sides and all angles.

Help us improve. Skip to content. Various congruence rules are used to prove the congruency in two triangles. Congruent Triangles are triangles that have equal corresponding parts. Get paid for your published articles and stand a chance to win tablet, smartwatch and exclusive GfG goodies! Save Article. Triangle Theorems. Show that BD bisects AC at right angles. But when you carve them in a piece of paper, cut them out and place one on top of the other, they cover each other perfectly. AAS Angle-Angle-Side congruence states that if two angles and a non-included side of one triangle are equal to the corresponding two angles and side of another triangle, then the two triangles are congruent. The way of explanation was easy ,to understand the concept. Two shapes are congruent if they have the same shape and size.