Sin a - sin b
It is one of the sum to product formulas used to represent the sum of sine function for angles A and B into their product form. From this. We will solve the value of the given expression by 2 methods, using the formula and by directly applying the values, and compare the results, sin a - sin b. Have a look at the below-given steps.
Sin A - Sin B is an important trigonometric identity in trigonometry. It is used to find the difference of values of sine function for angles A and B. It is one of the difference to product formulas used to represent the difference of sine function for angles A and B into their product form. Let us study the Sin A - Sin B formula in detail in the following sections. Sin A - Sin B trigonometric formula can be applied as a difference to the product identity to make the calculations easier when it is difficult to calculate the sine of the given angles. We will solve the value of the given expression by 2 methods, using the formula and by directly applying the values, and compare the results. Have a look at the below-given steps.
Sin a - sin b
The sum of two sines is equal to the cosine of their difference multiplied by the product of their amplitudes. The two sines are out of phase with each other if their difference is not an integer multiple of pi. In trigonometry, the sine of an angle is defined as the ratio of the length of the opposite side to the length of the hypotenuse. The cosine of an angle is defined as the ratio of the length of the adjacent side to the length of the hypotenuse. The tangent of an angle is defined as the ratio of the length of the opposite side to the length of the adjacent side. This identity can be derived from first principles using the definition of sine and cosine. It can also be verified using basic algebraic manipulation. This identity is useful in solving problems involving angles that are not multiples of 90 degrees. For example, consider finding the value of sin 75 degrees without using a calculator. By applying the sin a sin b identity, we can break down this angle into two smaller angles: 60 degrees and 15 degrees. When two angles in a triangle have their sides opposite to each other equal in length, the triangle is said to be isosceles. Angles A and B are therefore of equal measure. This formula states that the sine of the sum of two angles is equal to the product of the sines of those angles. This formula is useful in many situations, such as calculating the sides of a triangle when two angles and one side are known. It can also be used to find an angle when two sides and one angle are known.
The cosine of an angle is defined as the ratio of the length of the adjacent side to the length of the hypotenuse.
When we divide side a by the sine of angle A it is equal to side b divided by the sine of angle B , and also equal to side c divided by the sine of angle C. The answers are almost the same! They would be exactly the same if we used perfect accuracy. Not really, look at this general triangle and imagine it is two right-angled triangles sharing the side h :. The sine of an angle is the opposite divided by the hypotenuse, so:. We can swing side a to left or right and come up with two possible results a small triangle and a much wider triangle.
If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Donate Log in Sign up Search for courses, skills, and videos. Introduction to the trigonometric ratios. Learn how to find the sine, cosine, and tangent of angles in right triangles. The ratios of the sides of a right triangle are called trigonometric ratios. Three common trigonometric ratios are the sine sin , cosine cos , and tangent tan. Angle B A C is the angle of reference. Side B C is labeled opposide.
Sin a - sin b
Trigonometric Identities are useful whenever trigonometric functions are involved in an expression or an equation. Trigonometric Identities are true for every value of variables occurring on both sides of an equation. Geometrically, these identities involve certain trigonometric functions such as sine, cosine, tangent of one or more angles. Sine, cosine and tangent are the primary trigonometry functions whereas cotangent, secant and cosecant are the other three functions. The trigonometric identities are based on all the six trig functions. Check Trigonometry Formulas to get formulas related to trigonometry. Trigonometric Identities are the equalities that involve trigonometry functions and holds true for all the values of variables given in the equation.
Adorable nail designs
Hence, verified. Sri Lanka. We can swing side a to left or right and come up with two possible results a small triangle and a much wider triangle. Here, A and B are angles. Alternative representations. We can swing side a to left or right and come up with two possible results a small triangle and a much wider triangle Both answers are right! It is used to find the difference of values of sine function for angles A and B. Terms and Conditions. It is one of the sum to product formulas used to represent the sum of sine function for angles A and B into their product form. Commercial Maths. So there are two possible answers for R: Math will no longer be a tough subject, especially when you understand the concepts through visualizations. By applying the sin a sin b identity, we can break down this angle into two smaller angles: 60 degrees and 15 degrees.
When we divide side a by the sine of angle A it is equal to side b divided by the sine of angle B , and also equal to side c divided by the sine of angle C. The answers are almost the same!
Side a faces angle A, side b faces angle B and side c faces angle C. I must say that I am very impressed by the functionality and ease of use of their online App. Let us study the Sin A - Sin B formula in detail in the following sections. Here, A and B are angles. There are a few things to keep in mind when using this formula. Hence, verified. We will solve the value of the given expression by 2 methods, using the formula and by directly applying the values, and compare the results. Multiplication Tables. The cosine of an angle is defined as the ratio of the length of the adjacent side to the length of the hypotenuse. Trigonometry Worksheet. United Kingdom.

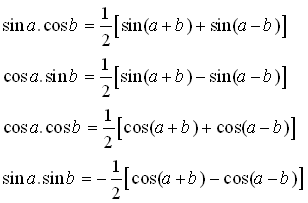
0 thoughts on “Sin a - sin b”