Vector space calculator
Didn't find the calculator you need? Request it.
The calculator will find a basis of the space spanned by the set of given vectors, with steps shown. The Basis Calculator is an advanced online resource specifically designed to find the basis of a vector space. The calculator aims to ease your mathematical journey by providing quick, precise, and correct results. Thus, it allows you to concentrate on the comprehension of concepts instead of diving into complicated calculations. The calculator will immediately compute and display the result, i. In the realm of linear algebra, the notion of the basis of a vector space is an essential building block. The basis for a vector space is defined as a set of vectors that satisfy two key conditions:.
Vector space calculator
We use cookies to improve your experience on our site and to show you relevant advertising. By browsing this website, you agree to our use of cookies. Learn more. Share this solution or page with your friends. Support us. New All problem can be solved using search box. I want to sell my website www. What's new. College Algebra. Numerical Methods. Statistical Methods. Operation Research. Word Problems. Multiplication of two matrix 3. Division of two matrix 4.
Often, vector space calculator, when drawing the forces that act on an object, like velocity or gravitational pull, we use straight arrows to describe their direction and valueand that's where the " arrow definition " comes from. This free online calculator help you to understand is the entered vectors a basis.
Welcome to the linear independence calculator , where we'll learn how to check if you're dealing with linearly independent vectors or not. In essence, the world around us is a vector space and sometimes it is useful to limit ourselves to a smaller section of it. For example, a sphere is a 3-dimensional shape , but a circle exists in just two dimensions , so why bother with calculations in three? Linear dependence allows us to do just that - work in a smaller space, the so-called span of the vectors in question. But don't you worry if you've found all these fancy words fuzzy so far. In a second, we'll slowly go through all of this together.
A vector space is a set that is closed under finite vector addition and scalar multiplication. The basic example is -dimensional Euclidean space , where every element is represented by a list of real numbers, scalars are real numbers, addition is componentwise, and scalar multiplication is multiplication on each term separately. For a general vector space, the scalars are members of a field , in which case is called a vector space over. Euclidean -space is called a real vector space , and is called a complex vector space. In order for to be a vector space, the following conditions must hold for all elements and any scalars :. Associativity of vector addition :.
Vector space calculator
Linear algebra uses the tools and methods of vector and matrix operations to determine the properties of linear systems. Wolfram Alpha's rigorous computational knowledge of topics such as vectors, vector spaces and matrix theory is a great resource for calculating and exploring the properties of vectors and matrices, the linear independence of vectors and the vector spaces underlying sets of vectors and matrices. Find properties of and perform computations on n -dimensional vectors. Check vectors for both linear dependence and linear independence. Explore various properties of matrices. Compute properties of linear vector spaces. Uh oh! Wolfram Alpha doesn't run without JavaScript. Please enable JavaScript. If you don't know how, you can find instructions here.
Downtown brooklyn emf experiments
This free online calculator help you to understand is the entered vectors a basis. The calculator will find the transition matrix from the first basis to the second basis, with steps shown. Scalar Multiplication of vectors 3. Once we input the last number, the linear independence calculator will instantly tell us if we have linearly independent vectors or not , and what is the dimension of the span of the vectors. Cholesky Decomposition What's new. Singular Value Decomposition Calculator The calculator will find the singular value decomposition SVD of the given matrix, with steps shown. On the other hand, the property of spanning the vector space means that every vector in the space can be expressed as a linear combination of the basis vectors. Cofactor of a matrix As we've seen in the above section , we can add them and multiply them by scalars. But let's leave that abstract mumbo-jumbo to scientists. The calculator will multiply the given matrix by the given scalar, with steps shown. If you want to contact me, probably have some questions, write me using the contact form or email me on [email protected].
This calculator performs all vector operations in two and three dimensional space. You can add, subtract, find length, find vector projections, find dot and cross product of two vectors.
Examples for Linear Algebra Linear algebra uses the tools and methods of vector and matrix operations to determine the properties of linear systems. Diagonalize Matrix Calculator The calculator will diagonalize the given matrix if possible , with steps shown. Welcome to the linear independence calculator , where we'll learn how to check if you're dealing with linearly independent vectors or not. Solving with steps. However, fortunately, we'll limit ourselves to two basic ones which follow similar rules to the same matrix operations vectors are, in fact, one-row matrices. Therefore, the rank of our matrix will simply be the number of non-zero rows of the array we obtained , which in this case is 2 2 2. Support us. You can verify if a set of vectors is linearly independent by computing the determinant of a matrix whose columns are the vectors you want to check. You're finally able to take pictures and videos of the places you visit from far above. It will also find the determinant, inverse, rref reduced row echelon form , null space, rank, eigenvalues, and eigenvectors and will multiply the matrix by a scalar. Minor of a matrix The concept of a basis is fundamental to understanding many properties of vector spaces, and it plays a critical role in various mathematical disciplines, physics, engineering, computer science, and more.

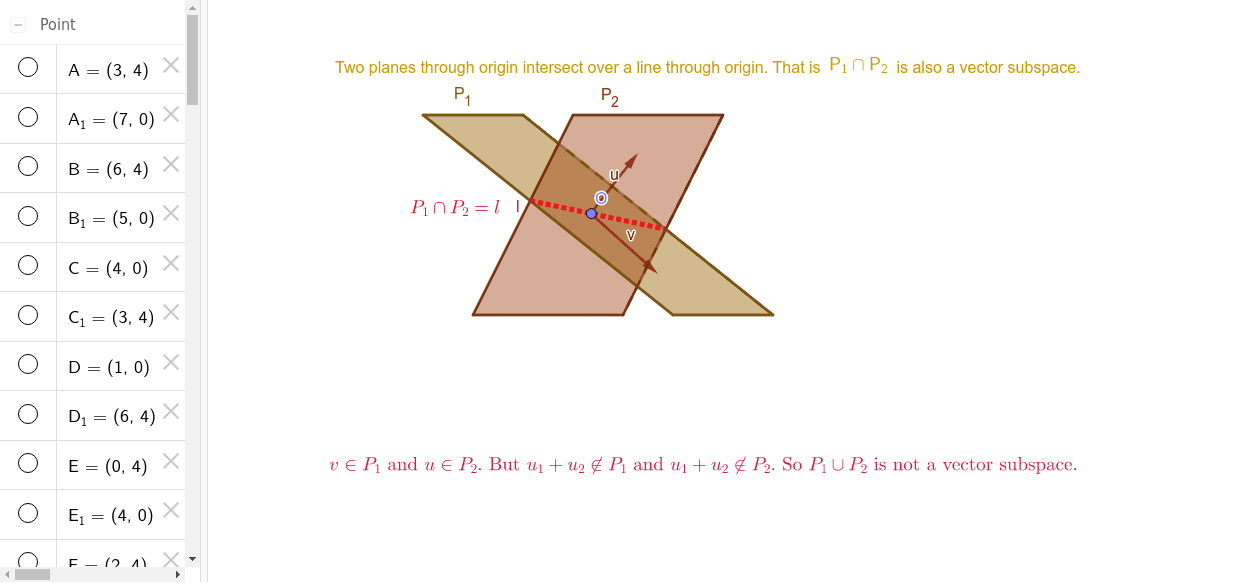
I think, that you are not right. Write to me in PM.