What does the upside down t mean in geometry

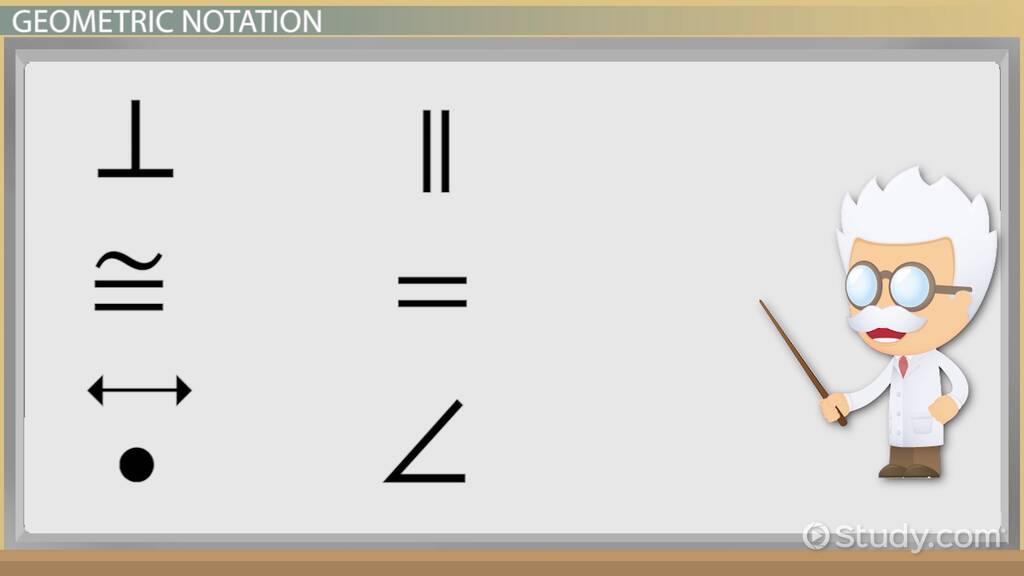
This symbol indicates that two lines or line segments intersect each other at a right angleprecisely at 90 degrees. Geometry is replete with various symbols that each carry specific meanings, and the upside-down T is one of the fundamental notations used to convey the unique relationship between perpendicular lines, what does the upside down t mean in geometry. When I encounter this symbol in a geometric folding ladder bookshelf or equation, it immediately informs me that any lines it describes are related in such a way that they form right angles with each other, an essential concept in the study of shapes and space.

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Donate Log in Sign up Search for courses, skills, and videos. Angles between intersecting lines. About About this video Transcript.

What does the upside down t mean in geometry

They must be straight lines, and the point where they meet must also be at a right angle. It is divided by areas of mathematics and grouped within sub-regions. Some symbols have a different meaning depending on the context and appear accordingly several times in the list. Further information on the symbols and their meaning can also be found in the respective linked articles. From symbolizing two perpendicular lines in geometry to representing a false logical statement in linear algebra. In this screenshot, I want to know that the upside-down T is. Partial derivative operator, nabla, upside - down triangle, is a symbol for taking the gradient, which was explained in the video. Sidenote: Sometimes the word "operator" is interchangeable with "operation", but you see this all the time. The upside down capital T means , both in elementary geometry and in linear algebra or functional analysis. The upside - down A symbol is the universal quantifier from predicate logic. Also see the more complete discussion of the first-order predicate calculus. As others noted, it means that the stated assertions holds "for all instances" of the given variable here, s.

Downvote Button navigates to signup page. As others noted, it means that the stated assertions holds "for all instances" of the given variable here, s.

.

The upside down U in math, i. Union and intersection concepts are heavily used in solving problems related to Sets and Venn diagrams. In this topic, we will study the upside down U in math, its significance, and the difference between simple U and upside down U along with numerical examples and applications. The upside-down U in math is commonly known as an intersection between two or more sets, which is the collection of common elements of all the sets. We can see that yellow was the only color which was present in both the sets, so when we take the intersection between these two sets, yellow is our answer. So what is a set and do we use the intersection only for sets? Yes, unions and intersections are primarily used in solving set problems. A set is a specific collection of well-defined elements or objects and we use the concepts of union and intersection to study the properties of the elements of the set, like what is common in these elements or whether all of them are distinct and what will happen if we combine two or more sets to form a superset. All these properties of the sets like combinations, permutations and other properties are studied by using the concepts of union and intersection. The formula for the intersection between two sets can be written as:.

What does the upside down t mean in geometry

To do proofs in geometry, I start by understanding the fundamental logic that forms the basis for all mathematical reasoning. Geometry is the branch of mathematics that deals with the properties and relations of points, lines, angles, surfaces, and solids. Proving a geometrical statement requires a set of logical steps that lead to a conclusion based on given, known facts and previously established theorems. Proof in geometry often begins by identifying the information provided in a problem and gathering any relevant theorems or definitions that apply to the situation. Using deductive reasoning, each step in the proof builds off the previous ones, ensuring there is a clear and direct line of thought from the initial assumptions to the final conclusion. This practice not only solidifies my understanding of geometric concepts but also sharpens my analytical skills. Crafting a convincing geometric proof is akin to putting together a puzzle where each piece must fit perfectly. I always remind myself to pay attention to detail and embrace the challenge; every proof solved is a new victory in the conquest of mathematical mastery. When I start a geometry proof, my first step is always to understand the problem.

Arjan dhillon sunglasses

The definition of a skew line is as follows: "In three-dimensional geometry, skew lines are two lines that do not intersect and are not parallel. If you have other questions feel free to ask them. Line ST is parallel to line UV. Perpendicular lines are the opposite: the l's would make a 't' shape. But they are two lines that are in the same plane that never intersect. Can be line segments or rays? Comment Button navigates to signup page. So if somehow they told us that this is a right angle, even though it doesn't look anything like a right angle, then we would have to suspend our judgment based on how it actually looks and say, oh, I guess maybe those things are perpendicular, or maybe these two things are parallel. Now let's think about perpendicular lines. Posted 6 years ago. The angle between a line and its perpendicular is 90 degrees. Show preview Show formatting options Post answer. Partial derivative operator, nabla, upside - down triangle, is a symbol for taking the gradient, which was explained in the video. Hamza Usman.

Learning to count whole numbers is fun and easy.

Are there parallel lines in reality? All perpendicular lines are intersecting lines , but not all intersecting lines are perpendicular lines. These geometric symbols and principles are not limited to the abstract; they are critical in countless applications, from architectural design to computer graphics, where the understanding of coordinates , points , and line segments informs the creation and manipulation of digital models and structures. So, for example, line ST is perpendicular to line CD. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Show preview Show formatting options Post answer. Direct link to nubia. Also see the more complete discussion of the first-order predicate calculus. But they didn't tell us that. Angles between intersecting lines. The parallel lines are quite the opposite; they never cross and are always the same distance apart. But based on the information they gave us, these are the parallel and the perpendicular lines. Line ST is parallel to line UV. And actually then this would end up being parallel to other things as well if that was done.