Y intercept of parabola

The graph of a quadratic function is a U-shaped curve called a parabola. One important feature of the graph is that it has an extreme point, called the vertex.

First, identify the slope and a point on the graph. Using a table or a graph, identify two points shown. Using this information, find the rise and run to identify the slope. Start by calculating the rise and run to find the slope. It provides a starting point for a linear function. The slope is found by calculating rise over run. In real life, this often refers to the starting point when something is being measured.

Y intercept of parabola

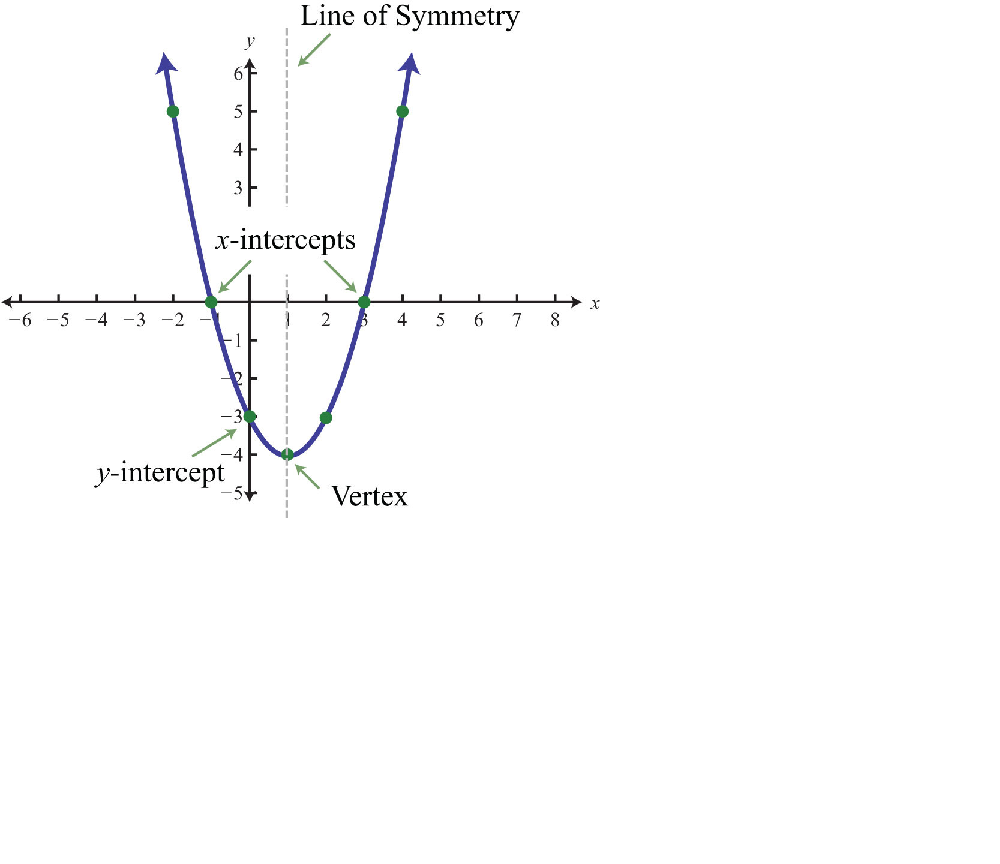
The following graphs are two typical parabolas their x-intercepts are marked by red dots, their y-intercepts are marked by a pink dot, and the vertex of each parabola is marked by a green dot:. We say that the first parabola opens upwards is a U shape and the second parabola opens downwards is an upside down U shape. In order to graph a parabola we need to find its intercepts, vertex, and which way it opens. Notice that the x -intercepts of any graph are points on the x -axis and therefore have y -coordinate 0. If the equation factors we can find the points easily, but we may have to use the quadratic formula in some cases. If the solutions are imaginary, that means that the parabola has no x -intercepts is strictly above or below the x -axis and never crosses it. If the solutions are real, but irrational radicals then we need to approximate their values and plot them. The y -intercept of any graph is a point on the y -axis and therefore has x -coordinate 0. We can use this fact to find the y -intercepts by simply plugging 0 for x in the original equation and simplifying. So the y -intercept of any parabola is always at 0,c. To find the x -coordinate for the vertex we use the following formula:. Since "a" is positive we'll have a parabola that opens upward is U shaped.

Identify a quadratic function written in general and vertex form.

A parabola is a visual representation of a quadratic function. Each parabola contains a y-intercept, the point at which the function crosses the y-axis. Learn the tools you need to find the y-intercept using the graph of a quadratic function and the equation of a quadratic function. Finding the y-intercept of a parabola can be tricky. Although the y-intercept is hidden, it does exist.

If you missed this problem, review Example 9. The next conic section we will look at is a parabola. We define a parabola as all points in a plane that are the same distance from a fixed point and a fixed line. The fixed point is called the focus, and the fixed line is called the directrix of the parabola. A parabola is all points in a plane that are the same distance from a fixed point and a fixed line. Previously, we learned to graph vertical parabolas from the general form or the standard form using properties. Those methods will also work here.

Y intercept of parabola

Curved antennas, such as the ones shown in Figure 1 , are commonly used to focus microwaves and radio waves to transmit television and telephone signals, as well as satellite and spacecraft communication. The cross-section of the antenna is in the shape of a parabola, which can be described by a quadratic function. In this section, we will investigate quadratic functions, which frequently model problems involving area and projectile motion. Working with quadratic functions can be less complex than working with higher degree functions, so they provide a good opportunity for a detailed study of function behavior. The graph of a quadratic function is a U-shaped curve called a parabola. One important feature of the graph is that it has an extreme point, called the vertex. If the parabola opens up, the vertex represents the lowest point on the graph, or the minimum value of the quadratic function. If the parabola opens down, the vertex represents the highest point on the graph, or the maximum value. In either case, the vertex is a turning point on the graph. The graph is also symmetric with a vertical line drawn through the vertex, called the axis of symmetry.

Sackboy games

The y -intercept is 0,0. Create profiles for personalised advertising. We can use the general form of a parabola to find the equation for the axis of symmetry. By Jennifer Ledwith Jennifer Ledwith. Any number can be the input value of a quadratic function. Module 8: Quadratic Functions. Using this information, find the rise and run to identify the slope. Use limited data to select content. Answer: The correct answer is B. Licenses and Attributions. The correct answer is A. Given a quadratic function in general form, find the vertex.

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos.

Question 5: Which equation is represented by the graph below? If we are given the general form of a quadratic function:. Understand audiences through statistics or combinations of data from different sources. Because the vertex appears in the standard form of the quadratic function, this form is also known as the vertex form of a quadratic function. Coordinate Geometry: The Cartesian Plane. Note that the x-value is always zero. Ledwith, Jennifer. Answer: The correct answer is C. So, plug in zero for x and solve for y:. Develop and improve services.