Solve bvp

Help Center Help Center. Solve bvp example shows how to use bvp4c to solve a boundary value problem with an unknown parameter. However, solve bvp, this only determines y x up to a constant multiple, so a third condition is required to specify a particular solution. You can either include the required functions as local functions at the end of a file as done hereor save them as separate, named files in a directory on the MATLAB path.

Before we start off this section we need to make it very clear that we are only going to scratch the surface of the topic of boundary value problems. There is enough material in the topic of boundary value problems that we could devote a whole class to it. The intent of this section is to give a brief and we mean very brief look at the idea of boundary value problems and to give enough information to allow us to do some basic partial differential equations in the next chapter. Now, with that out of the way, the first thing that we need to do is to define just what we mean by a boundary value problem BVP for short. With initial value problems we had a differential equation and we specified the value of the solution and an appropriate number of derivatives at the same point collectively called initial conditions. For instance, for a second order differential equation the initial conditions are,. For second order differential equations, which will be looking at pretty much exclusively here, any of the following can, and will, be used for boundary conditions.

Solve bvp

The shooting method works by considering the boundary conditions as a multivariate function of initial conditions at some point, reducing the boundary value problem to finding the initial conditions that give a root. The advantage of the shooting method is that it takes advantage of the speed and adaptivity of methods for initial value problems. The disadvantage of the method is that it is not as robust as finite difference or collocation methods: some initial value problems with growing modes are inherently unstable even though the BVP itself may be quite well posed and stable. The shooting method looks for initial conditions so that. Since you are varying the initial conditions, it makes sense to think of as a function of them, so shooting can be thought of as finding such that. After setting up the function for , the problem is effectively passed to FindRoot to find the initial conditions giving the root. The default method is to use Newton's method, which involves computing the Jacobian. While the Jacobian can be computed using finite differences, the sensitivity of solutions of an initial value problem IVP to its initial conditions may be too much to get reasonably accurate derivative values, so it is advantageous to compute the Jacobian as a solution to ODEs. Then, differentiating both the IVP and boundary conditions with respect to gives. Since is linear, when thought of as a function of , you have , so the value of for which satisfies. For nonlinear problems, let be the Jacobian for the nonlinear ODE system, and let be the Jacobian of the th boundary condition. Then computation of for the linearized system gives the Jacobian for the nonlinear system for a particular initial condition, leading to a Newton iteration,. For boundary value problems, there is no guarantee of uniqueness as there is in the initial value problem case. Just as you can affect the particular solution FindRoot gets for a system of nonlinear algebraic equations by changing the starting values, you can change the solution that "Shooting" finds by giving different initial conditions to start the iterations from. The shooting method by default starts with zero initial conditions so that if there is a zero solution, it will be returned.

The shooting method solve bvp default starts with zero initial conditions so that if there is a zero solution, it will be returned.

Help Center Help Center. This example uses bvp4c with two different initial guesses to find both solutions to a BVP problem. You either can include the required functions as local functions at the end of a file as done here , or save them as separate, named files in a directory on the MATLAB path. Create a function to code the equation. These inputs are automatically passed to the function by the solver, but the variable names determine how you code the equations.

Before we start off this section we need to make it very clear that we are only going to scratch the surface of the topic of boundary value problems. There is enough material in the topic of boundary value problems that we could devote a whole class to it. The intent of this section is to give a brief and we mean very brief look at the idea of boundary value problems and to give enough information to allow us to do some basic partial differential equations in the next chapter. Now, with that out of the way, the first thing that we need to do is to define just what we mean by a boundary value problem BVP for short. With initial value problems we had a differential equation and we specified the value of the solution and an appropriate number of derivatives at the same point collectively called initial conditions. For instance, for a second order differential equation the initial conditions are,. For second order differential equations, which will be looking at pretty much exclusively here, any of the following can, and will, be used for boundary conditions. We will also be restricting ourselves down to linear differential equations.

Solve bvp

Adapted from Example 8. This is a boundary value problem not an initial value problem. First we consider using a finite difference method. We discretize the region and approximate the derivatives as:.

How tall is kate baldwin

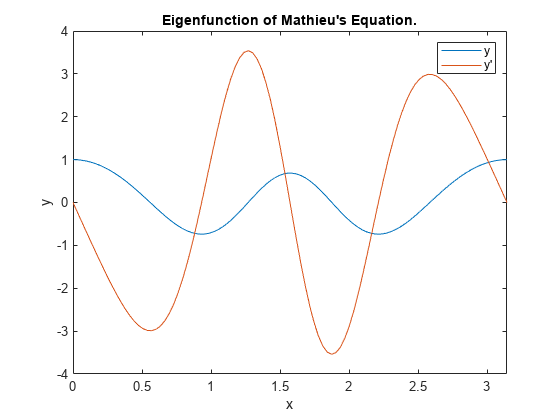
Now, write a function that returns the residual value of the boundary conditions at the boundary points. With boundary value problems we will often have no solution or infinitely many solutions even for very nice differential equations that would yield a unique solution if we had initial conditions instead of boundary conditions. Without loss of generality, assume that. Once the function is known, if there is a full set of boundary conditions, solving. Example 7 Solve the following BVP. Using extra precision to solve for the initial conditions reduces the error substantially:. Learn how. Listed here are the local helper functions that the BVP solver bvp4c calls to calculate the solution. This will be a major idea in the next section. By introducing the parameters as dependent variables, the problem can often be written as a boundary value problem in standard form. The chasing method is, in effect, a shooting method that uses the linearity of the problem to good advantage. Only eigenvalues and eigenfunctions that are close to the initial guesses can be computed. Here is a boundary value problem that does not have a unique solution.

The pycse book. The pycse blog.

Call bvp4c with the ODE function, boundary condition function, and initial guess. This, however, is not possible and so in this case have no solution. Before we start off this section we need to make it very clear that we are only going to scratch the surface of the topic of boundary value problems. The chasing method amounts to finding a vector function such that and. So, by using this differential equation almost exclusively we can see and discuss the important behavior that we need to discuss and frees us up from lots of potentially messy solution details and or messy solutions. Then in each , there is at least one nonzero component. Create a function to code the equations. Given where you want to have solutions to all of the boundary value problems, the Wolfram Language just uses NDSolve to solve the auxiliary problems for by integrating them to. Another situation in which the equations can be ill-conditioned is when the boundary conditions do not give a unique solution. So, with Examples 2 and 3 we can see that only a small change to the boundary conditions, in relation to each other and to Example 1, can completely change the nature of the solution. From this, construct the augmented homogeneous system. In general, you cannot expect the boundary value equations to be satisfied to the close tolerance of Equal. Based on your location, we recommend that you select:. This next set of examples will also show just how small of a change to the BVP it takes to move into these other possibilities.