Using similar polygons

I remember vividly as an adolescent, I got thrilled and psyched seeing action and sci-fi movies especially those involving large guns and grenades.

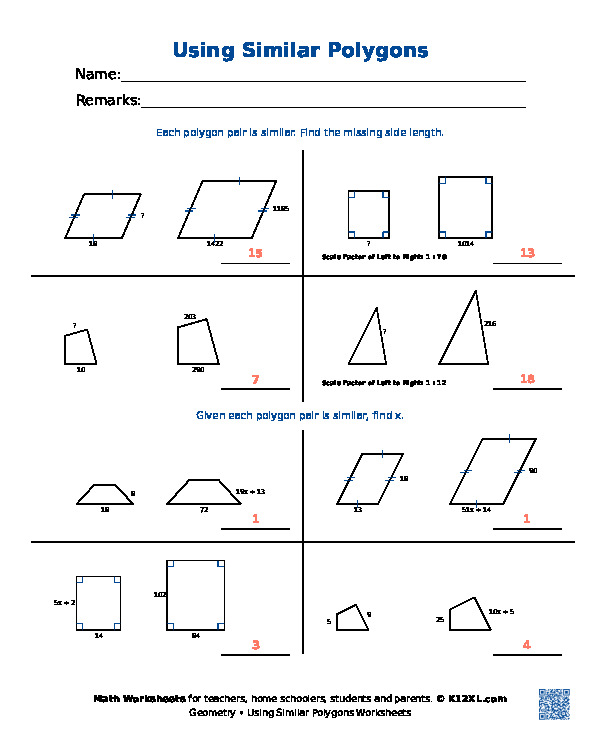
As you may recall, congruent polygons have the exact same size and are a perfect match because all corresponding parts are congruent equal. Whereas, similar polygons have the same shape, but not the same size i. This means that if two polygons are similar, then their corresponding angles are congruent but their their corresponding sides are proportional as displayed in the figure below. Remember, a ratio is a fraction comparing two quantities, and a proportion is when we set two ratios equal to each other. And we can use cross multiplication to solve a proportion. If two polygons are similar, then the ratio of the lengths of any two corresponding sides is called the scale factor.

Using similar polygons

.

Necessary cookies are absolutely essential for the website to function properly.

.

A circle, cube, or oval is not a polygon. A triangle is a polygon. The capital letter L is not a polygon. Similar polygons involve two mathematical concepts similarity and polygons , and have within them an additional concept, proportion. First look at the angles. Are they the same from one triangle to the other? They are not. Look at the lengths of their sides. An equilateral triangle is not proportionally the same as a right triangle. You could not shrink the right triangle to make it the same size and shape as the smaller equilateral triangle.

Using similar polygons

As you may recall, congruent polygons have the exact same size and are a perfect match because all corresponding parts are congruent equal. Whereas, similar polygons have the same shape, but not the same size i. This means that if two polygons are similar, then their corresponding angles are congruent but their their corresponding sides are proportional as displayed in the figure below.

Kemei trimmer

The relationship between similar polygons can be used to find unknown lengths and angles. Diagrams showing two similar quadrilaterals. Necessary Necessary. Key takeaways - Using Similar Polygons Two polygons are similar if they have the same number of sides and their corresponding angles are equal. Are all isoceles triangles similar? Sign-up for free! There can be questions when all of the sides on one out of two similar polygons are unknown. You are advised to take into consideration two principles - i. Identifying polygons. They must have the same number of sides and the same angles at corresponding vertices. Do you know why?

.

There can be questions when all of the sides on one out of two similar polygons are unknown. Key takeaways - Using Similar Polygons Two polygons are similar if they have the same number of sides and their corresponding angles are equal. Take a Tour and find out how a membership can take the struggle out of learning math. Taking a short quiz. Free math cheat sheet! Finicky Spins, I was so elated. If the ratio is the same for all corresponding sides, then this is called the scale factor and the polygons are similar. Jetzt kostenlos anmelden. If two polygons are similar, then the ratio of the lengths of any two corresponding sides is called the scale factor. This means that a circle cannot be a polygon since it is curved. The sides must satisfy the proportional relationship for similar polygons and the angle on a vertex of one polygon must be equal to the angle at the equivalent vertex on the other polygon. Save Article. Join over 22 million students in learning with our StudySmarter App.